III. Method to label the head

Labeling the head tetrahedra with labels BRAIN, SKULL or SCALP

1. General method

The principle of the method is based on the following remarks: an interior tetrahedron t (i.e. for example a tetrahedron t of the head H only composed of BRAIN and such that all its neighbors are also only composed of BRAIN) is homotopic to a full sphere as the brain. The set (H \ {t}) is homotopic to an empty sphere, as are the scalp and the skull.
So we will use homotopic deformations of the sets {t} and (H \ {t}) to label the different tetrahedra.

2. Labeling processes for the scalp and the skull

The skull and the scalp are both homotopic to an empty sphere, so they are homotopic to the set (H \ {t}).
First, we will label the most exterior component of the head: the scalp. The principle is an interior erosion of the set (H \ {t}) until stability, i.e. until there is no more removable tetrahedron. For example, if we apply an interior erosion on the set H until there is no more simple tetrahedron, we obtain the set, called homotopic core (denoted by hc), in the following figure.

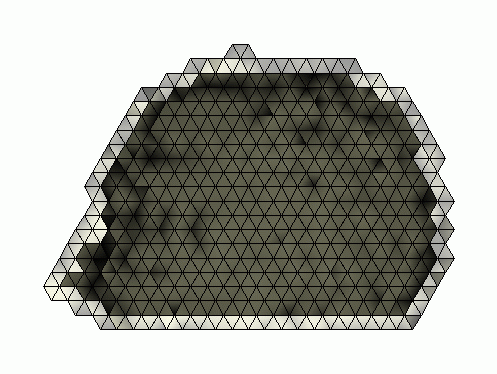
Result of the interior erosion of the head until there is no more simple tetrahedron:
light gray <-> homotopic core, dark gray <-> interior of the homotopic core.

As indicated in the figure, the dark gray part is the interior of the homotopic core, i.e. it is the set of removed tetrahedra during the erosion. Moreover, if we remove a tetrahedron from the homotopic core hc, we create a hole connecting the two sets separated by hc (the interior and the background), and so we change the topology of hc.
To label the scalp, we stop the erosion before reaching the homotopic core. Indeed, we do not want to remove tetrahedra that will belong to the scalp component. Then, during the erosion, we do not remove the tetrahedra containing more than a minimum given proportion of scalp. So we define a threshold mu_scalp (%) for the scalp composition: if the proportion of scalp in the current tetrahedron is superior to mu_scalp, even if it is a simple tetrahedron, we do not remove it from the set. Then we obtain the set Sc composed of tetrahedra belonging to the scalp, and we label these tetrahedra with the label SCALP.

The process is the same for the obtention of the skull: we apply an interior erosion to the set (H \ Sc) from an interior tetrahedron t and using a threshold mu_skull. Thus we obtain the set Sk composed of tetrahedra belonging to the skull, and we label these tetrahedra with SKULL.

3. Labeling process for the brain

To label the brain, we just have to consider the interior set obtained after the labeling of the skull. Indeed, this set is homotopic to the initial interior tetrahedron, so it is homotopic to a full sphere. Then, this set B is composed of tetrahedra belonging to the brain, and they are labeled with BRAIN.

I. Introduction II. Topological tools III. Method to label the head IV. First results and remarks V. Results with n=5 VI. Numerical values VII. Visible Human with CSF

Main page