II. Tools for homotopic labeling
1. Initialization
First we must find the set of tetrahedra H composing the head
among
the whole tetrahedra of the ART volume.
After, among the tetrahedra of H, we have to
label each tetrahedron as BRAIN, SKULL or SCALP,
according to the MRI segmented volume.
Before labeling, we compute for each tetrahedron the tissue composition:
a 4-cell array
Ax is associated to each tetrahedron x,
each cell
containing a percentage that is computed from the segmented volume.
The first cell of Ax contains the percentage
of BACKGROUNG in x, the second one contains the pourcentage
of BRAIN in x, the third one the percentage of SKULL in
x
and the last one the
percentage of SCALP in x. An example of Ax
can be: (0.00, 0.15, 0.65, 0.20).
The labeling is based on the notion
of simple tetrahedron.
2. Notion of simplicity
To have a good labeling of the different tissues of the head, we must
satisfy topological constraints. Indeed, we must conserve the topology of
the head structure, i.e. imbricated spheres:
the brain is homotopic to a full sphere; the brain is contained
in the skull that is homotopic to an empty sphere; the skull is
contained in the scalp that is homotopic to an empty sphere too.
To conserve these topological properties, we use
homotopic deformations (dilations or erosions) based on the notion
of simple tetrahedron:
A tetrahedron t is simple in a set of
tetrahedra X if its removal from X
(i.e. its addition to the
complementary Y of X in the space) does
not modify the topology of X nor of Y.
Then we have the following definition :
An homotopic erosion (resp. homotopic
dilation) of a set of tetrahedra
X is
obtain by a sequential removal (resp. addition) in X
of simple tetrahedra.
In his PhD thesis, J. Pescatore has given a local characterization
of the simplicity of a tetrahedron, allowing us to define an
erosion (or dilation) algorithm. He also proposed a labeling
algorithm based on an homotopic dilation, but this algorithm did not
guarantee that the labeled components corresponding to the
skull and the scalp were homotopic to empty spheres.
So we will propose another labeling algorithm guaranteeing the
conservation of the topology of the different tissues.
3. An example of homotopic dilation
Before labeling the head tetrahedra with the corresponding tissue labels,
we have to determine the tetrahedra belonging to the head or to the
background, considering that the whole head is homotopic
to a full sphere.
As a single tetrahedron is also homotopic to a full sphere, we decide
to dilate a set initially containing a single tetrahedron t
that is only composed
of BRAIN (according to the earlier computation of the tissue composition
At
for each tetrahedron x:
At=(0.00, 0.00, 0.00, 1.00)) and such that its
neighbors are also
only composed of BRAIN. The we apply an homotopic dilation of t
by adding simple tetrahedra that have a non-null composition of
at least one of the component on the head (i.e. BRAIN, SKULL or
SCALP).
One result of this strategy is presented in the following figure.
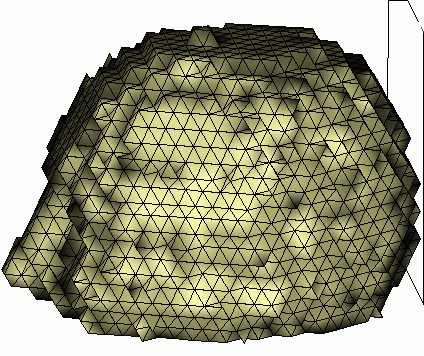
ART volume of a human head, n=4.
Now that we know the tetrahedra composing the head,
we must label these tetrahedra with the corresponding tissues.
I. Introduction
II. Topological tools
III. Method to label the head
IV. First results and remarks
V. Results with n=5
VI. Numerical values
VII. Visible Human with CSF
Main page

