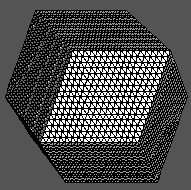Homotopic labeling of head tetrahedra

I. Introduction

1. Goal

In applications based on Electroencephalography (EEG) and Magnetoencephalography (MEG), electromagnetic field propagation is numerically calculated, for example using finite element methods. This computation is based on a meshed model of the head tissues. In this site, we propose a method to obtain such head models.
In our model, the head will be composed of identical tetrahedra, each tetraheron being labeled with the corresponding anatomical tissues: BRAIN, SKULL... Our labeling is done under topological constraints in order to respect the topological arrangement of the head, i.e. interwoven spheres.
We first present a method to decompose a part of the space into tetrahedra (see next paragraphs). Then, we introduce the notion of simple tetrahedron that allows us to propose the definition of homotopic deformations (see Topological tools). Finally, we explain the method we use to label the tetrahedra of the head using the homotopic deformations (see Method to label the head); some results and comments are also presented (see Results and remarks, Results with n=5, Numerical values).

2. Material

The data we have consist of a MRI volume representing a human head, and this image is segmented to extract anatomical tissues. Then this segmentation will be used for the labeling of the tetrahedra of the space at the following steps. We do not explain here in details the process used to obtain the segmented MRI from the initial image as it is not the goal of this site. A report of Elena Martinez-Perez (.pdf file) containing more explanations about the segmentation step can be downloaded here: report.

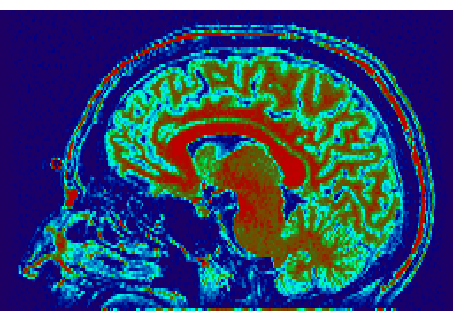
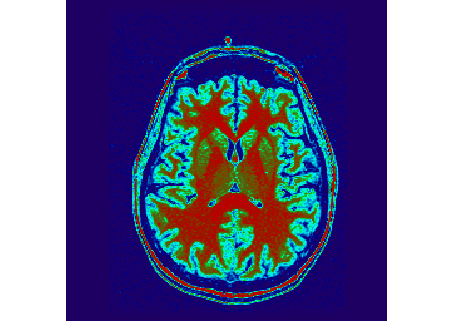
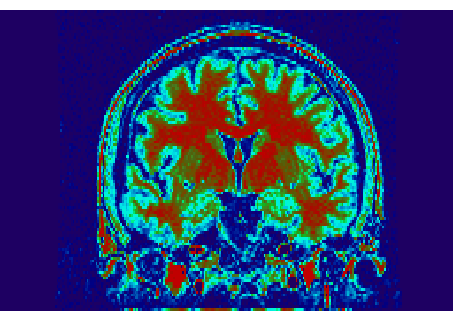
Initial MRI volume.

Segmented MRI volume:
dark blue <-> background, red <-> scalp, sky blue <-> skull, blue -> brain.
3. Tetrahedral decomposition of the space

We use a specific model called Almost Regular Tessalation (ART) volume mesh, based on the work of J. Pescatore during his PhD thesis. In this model, a portion of the space (that is a polyhedron) is composed of tetrahedra, each tetrahedron being close to an equilateral tetrahedron. This set of tetrahedra is obtained by successive subdivisions of the space that is initially a polyhedron P composed of 24 tetrahedra sharing a same vertex. This initial polyhedron contains the segmented MRI volume obtained before. At each step, each tetrahedron t composing P is subdivided into 8 tetrahedra congruent to t scaled by a factor 1/2. This process is proved to be subdivision invariant.
The number and the size of the obtained tetrahedra depend on the number n of successive subdivisions. The ART volumes presented here are obtained after n=4 subdivisions, and so the space is composed of 24*(8^n) = 98304 tetrahedra.

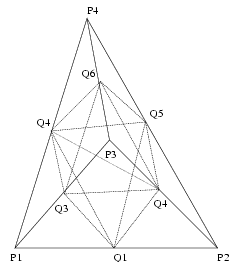
Subdivision of a tetrahedron

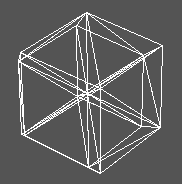
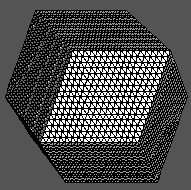
Successive subdivisions of the 24 initial tetrahedra representing the space and containing the head,
with from left to right: n=0 (24 tetraedra), n=1 (192 tetraedra), n=2 (1536 tetraedra) and n=4 (98304 tetraedra).
Based on this tetrahedral representation of the space, first we have to label the tetrahedra composing the head, and after we have to label each tetrahedron of the head with the corresponding anatomical tissue, from the MRI segmented volume.

I. Introduction II. Topological tools III. Method to label the head IV. FIrst results and remarks V. Results with n=5 VI. Numerical values VII. Visible Human with CSF

Main page