ERC Starting Grant COMNFT

The ERC Starting Grant ‘‘Communication Using the Nonlinear Fourier Transform (COMNFT)’’ is a research project funded by the the European Research Council (ERC), under the European Union's Horizon 2020 research and innovation program, grant agreement no. 805195.

The ERC work program supports ground-breaking high risk/high gain projects that go substantially beyond the state-of-the-art, awarded solely based on the scientific excellence. The overall goal of the COMNFT project is to develop a communication theory for a class of nonlinear channels such as optical fiber.

Summary of the project

The demand for data rate in communication networks has been increasing in the past few decades, with a compound annual growth rate (CAGR) of up to 80%. The growth of traffic is driven by the proliferation of the broadband services, applications and products, such as video streaming (eg, via Netflix), smartphones, cloud computing and services, data centers, and increasingly machine-to-machine communication and the Internet of Things.

Optical fiber forms the backbone of the communication networks, carrying most of the world's information traffic. Today, several billion kilometers of optical fibers have been deployed worldwide, connecting continents, cities and data centers. It is hard to overstate the importance of the fiber-optic systems to the information age that envelops us.

The exponential growth of traffic has brought about an escalating pressure on fiber-optic networks. It has been observed that the data rates in the optical transport networks have grown in recent decades with a CAGR that is notably less than the CAGR of the improvement in technologies that generate, process and store data. One factor is an important problem with the capacity of the optical fiber networks arising from the physics of optical fiber.

Optical fiber is a nonlinear medium, because its properties change with the signal intensity. The fiber Kerr nonlinearity makes the channel considerably different from the linear (eg, wireless) channels. Importantly, the achievable information rates (AIRs) of the current methods in optical fiber communication increase with the input signal power, reaching a peak at a certain optimal input power, and then asymptotically vanish as the power tends to infinity. This characteristic property of the information rates in fiber is in contrast to the capacity of the linear Gaussian channels that grows logarithmically with the signal power. It is widely believed that the fiber nonlinearity limits the AIRs of the conventional transmission methods. As a result, today's optical fiber networks face a looming ‘‘capacity crunch,’’ an emergency that drives technological advancement.

The objective of the ERC Starting Grant COMNFT is to establish the information-theoretic limits in optical fiber, and to develop communication algorithms that approach these limits. The project applies information theory and nonlinear Fourier transforms (NFTs) to understand the fiber nonlinearity and overcome the limitation that it sets on the transmission rates.

Work performed in the first period

The capacity of optical fiber to carry information has remained a vexing conundrum. Furthermore, the AIRs of the current methods such as WDM vanish at high powers due to treating interference (arising from the application of the linear multiplexing to the nonlinear channel) as noise. In this regard, the project made progress on the information-theoretic limits in optical fiber, and on the nonlinear frequency-division multiplexing (NFDM), a data transmission method based on the NFT.

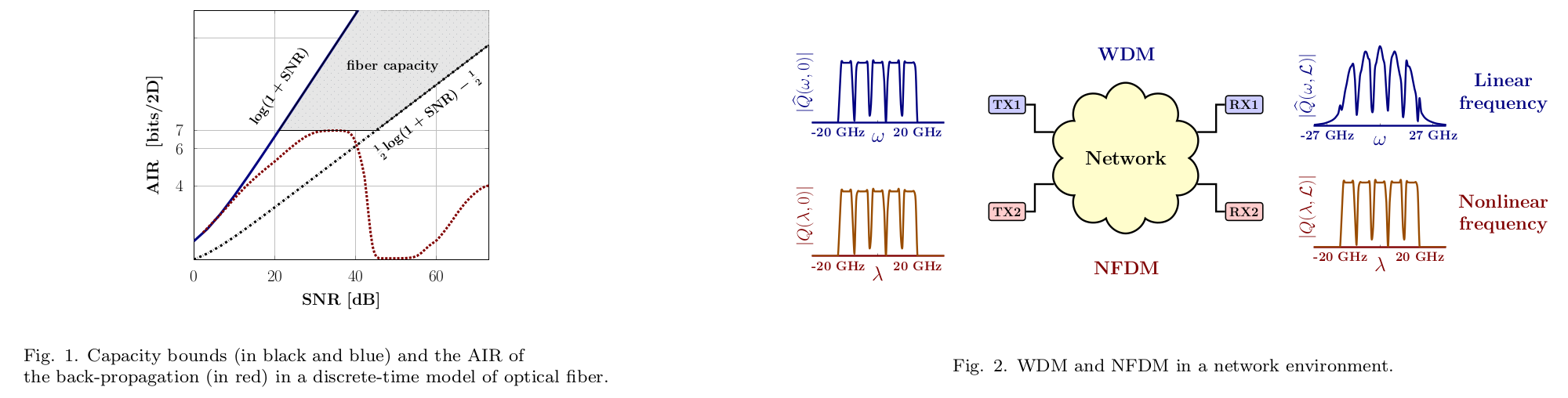
We considered a discrete-time continuous-space model of optical fiber described by the split-step Fourier method (SSFM), where the number of segments in distance K tends to infinity [1,2]. We showed that the capacity of this model is lower bounded as C >= (1/2) log(1 +SNR) - 1/2 + o(1) [1, Thm. 1]. As K is increased, the inter-symbol interference (ISI) averages out to zero and the SSFM model tends to a diagonal phase noise model. In this case, the number of degrees-of-freedom (DoFs) is at least half of the input dimension n. A number of similar lower bounds are obtained for other regimes [1,2]. The capacity pre-log is determined for finite K as well [1, Thm. 3].

We found that the AIR in the SSFM model with back-propagation follows a double-ascent curve. The AIR characteristically vanishes as the SNR is increased more than a certain value. However, if the SNR is further increased, the AIR will increase again, approaching the lower bound noted above; see Fig. 1.

We showed that the asymptotic capacity of the discrete-time discrete-space SSFM model of optical fiber when the SNR tends to infinity is doubly-logarithmic, i.e., C ~ (1/n) log(log(SNR)) + a, where a is a bounded offset [1,6]. In this case, there is only one DoF at high powers due to signal-noise interaction [1, Thm. 6]. The proof is based on the observation that as the SNR goes to infinity, the fiber model tends to a linear fading channel described by a random matrix.

We considered a zero-dispersion model of optical fiber, when the input is subject to a peak or an average cost constraint satisfying certain regularity conditions. We showed that the capacity is uniquely achieved by an input signal that has discrete amplitude, taking on finitely many values [4,5].

We compared the AIRs of the linear multiplexing represented by WDM and NFDM, shown in Fig. 1. We showed that the NFDM AIR is greater than the WDM AIR in a simplified system [3]. The result demonstrates that NFDM overcomes the nonlinearity limitation in this model.

Project personnel

Mansoor Yousefi, PI
Milad Sefidgaran, postdoc
Alireza Tasdighi, postdoc
Ibrahim Taha, PhD student

Publication

[1] M. Sefidgaran et al., ‘‘Lower bound on the capacity of the continuous-space SSFM model of optical fiber,’’ IEEE Trans. Inf. Theory, vol. 68, no. 4, pp. 2460–2478, Apr. 2022, doi:10.1109/TIT.2021.3139179.

[2] M. Sefidgaran et al., ‘‘On the capacity of the continuous-space SSFM model of optical fiber,’’ in IEEE Info. Theory Workshop, Apr. 2021 pp. 1-5, doi: 10.1109/ITW46852.2021.9457619.

[3] M. Yousefi et al., ‘‘Linear and Nonlinear Frequency-Division Multiplexing,’’ in IEEE Trans. Inf. Theory, vol. 66, no. 1, pp. 478-495, Jan. 2020, doi: 10.1109/TIT.2019.2941479.

[4] J. Fahs et al., ‘‘Capacity-Achieving Input Distribution in Per-Sample Zero-Dispersion Model of Optical Fiber,’’ IEEE Trans. Inf. Theory, vol. 67, no. 9, pp. 5840-5852, Sept. 2021, doi: 10.1109/TIT.2021.3095411

[5] J. Fahs et al., ‘‘On the Optimal Input of the Nondispersive Optical Fiber,’’ IEEE Int. Symp. Info. Theory, 2019, pp. 131-135, doi:10.1109/ISIT.2019.8849407

[6] M. Yousefi, ‘‘The asymptotic capacity of optical fiber,’’ arXiv:1610.06458, 2016.