A globally stable limit cycle that is locally unstable:
We consider a dynamical system in \(\mathbb{R}^3\) that is globally stable and locally instable,
this system is obtained by forcing the normal stable and unstable eigenvectors at each point on the limit cycle to undergo a rotation.
The differential equations of the system are given below (See [1]):
\begin{equation}
\begin{pmatrix}
\overset{.}{r}\\
\overset{.}{y}
\end{pmatrix}
= \mathbf{A}(\theta)
\begin{pmatrix}
r-1\\
y
\end{pmatrix}\\
\end{equation}
\begin{equation}
\overset{.}{\theta} = 0.01(1 + sin^2\theta)
\end{equation}
where:
\begin{equation}
\mathbf{A}(\theta) = \mathbf{R}
\begin{pmatrix}
\lambda_1 & 0 \\
0 & \lambda_2
\end{pmatrix}
\mathbf{R}^{-1}
\end{equation}
and
\begin{equation}
\mathbf{R} =
\begin{pmatrix}
cos(\omega z) & -sin(\omega z) \\
sin(\omega z) & cos(\omega z)
\end{pmatrix}
\end{equation}
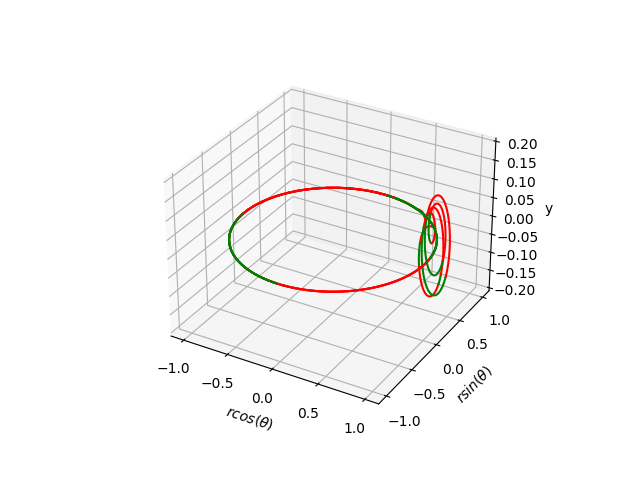
We consider the parameter values \(\lambda_1 = -1.1, \lambda_2 = 0.1, \omega = 30\) and initial condition
\(x(0) = (1.1, 0.1, 0) \)
Results:
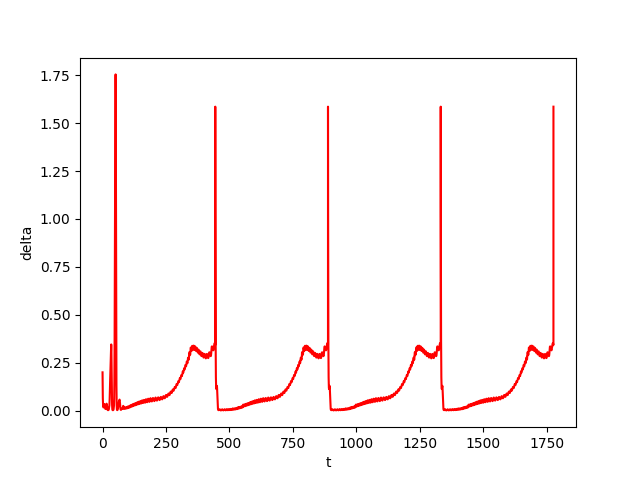
We consider a system with uncertainty \(w=0.01\), set of initial conditions \(B(x_0,\varepsilon)\) with \(\varepsilon=0.2\), the time-step used in Euler's method is \(\tau = 10^{-2}\), and we take \(T=k\tau\) with \(k=44430\) as an approximate period.
Using the figures shown below, we check that:
- \(B((i_0+1)T)\subset B(i_0T)\) for \(i_0=2\)
- and \(\Sigma_{i=1}^k\lambda_i\approx\) \(-5296< 0\).
Then, we can conclude that the system
converges towards an attractive LC
contained in
\([B(2T),B(3T)]\).
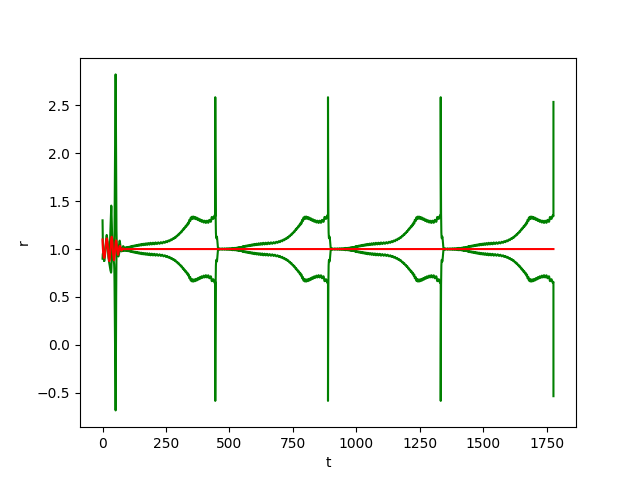
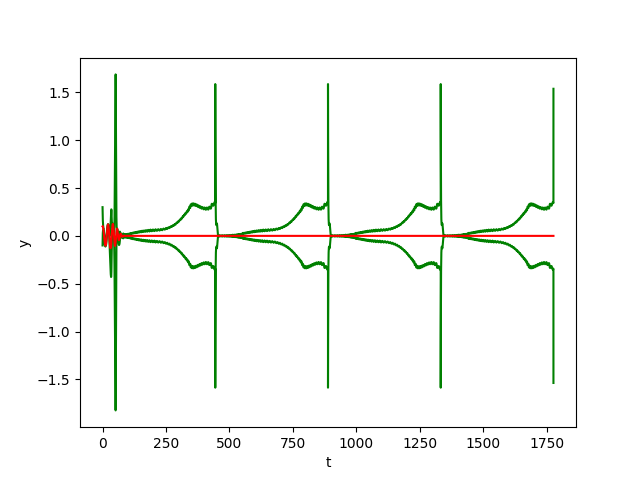
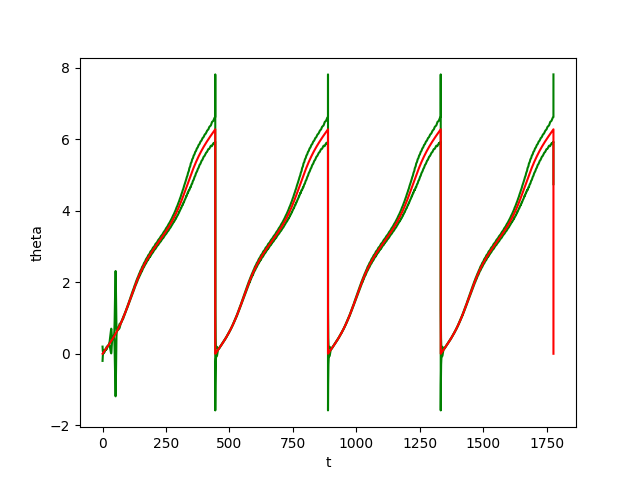
The figures below show respectively the simulation of \(r(t), y(t), \theta(t)\) and \(\delta_{{\cal W}}(t)\) with perturbation (w=0.01) over 4 periods (4T=1777.21) for dt=0.01.
In the figrues \(r(t)\) and \(y(t)\) and \(\theta(t)\), the red curves represent the Euler approximation and the green curves correspond to the borders of tube \(B\).
References:
[1] TALLAPRAGADA, Phanindra and SUDARSANAM, Senbagaraman. A globally stable attractor that is locally unstable everywhere. AIP Advances, 2017, vol. 7, no 12, p. 125012.




