Lorenz:
The following system of differential equations was introduced by Lorenz (see [1]):
\begin{cases}
\overset{.}{x_1} = -\sigma x_1 + \sigma x_2\\
\overset{.}{x_2} = \rho x_1 - x_2 - x_1 x_3\\
\overset{.}{x_3} = - \beta x_3 + x_1 x_2\\
\end{cases}
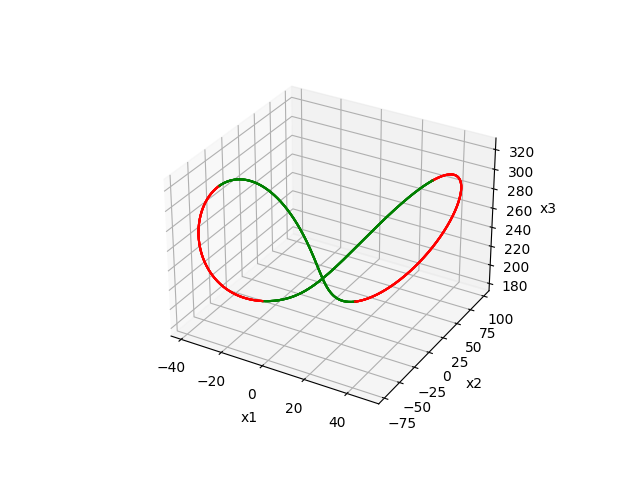
As a crude model of atmospheric dynamics, these equations led Lorenz to the discovery of sensitive dependence of initial conditions—an essential factor of unpredictability in many systems.
We consider: the classical parameter values \(\sigma = 10, \beta = 8/3\), \(\rho = 250\) and initial condition
\(x(0) = (16.21325444114593, -55.78140243373939, 249) \) (See [2])
Results:
We consider a system without uncertainty \(w=0\), set of initial conditions \(B(x_0,\varepsilon)\) with \(\varepsilon=350\), the time-step used in Euler's method is \(\tau = 10^{-5}\), and we take \(T=k\tau\) with \(k=46000\) as an approximate period.
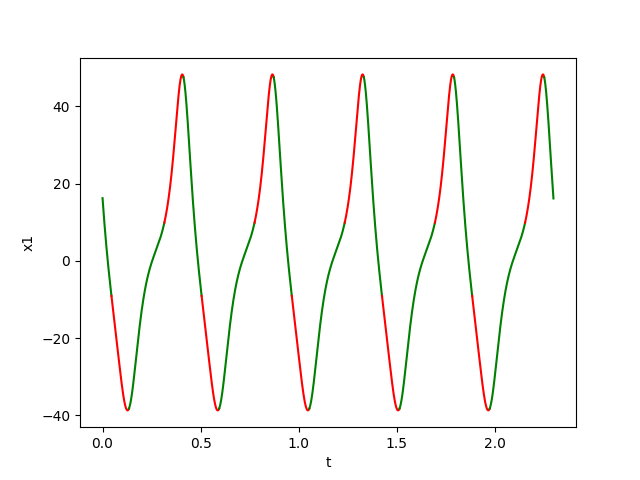
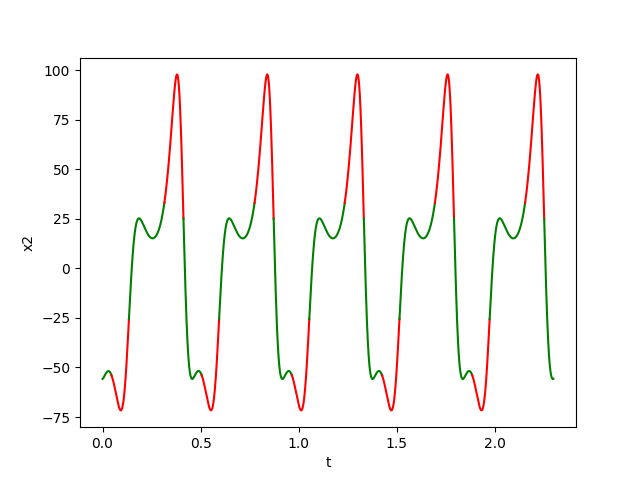
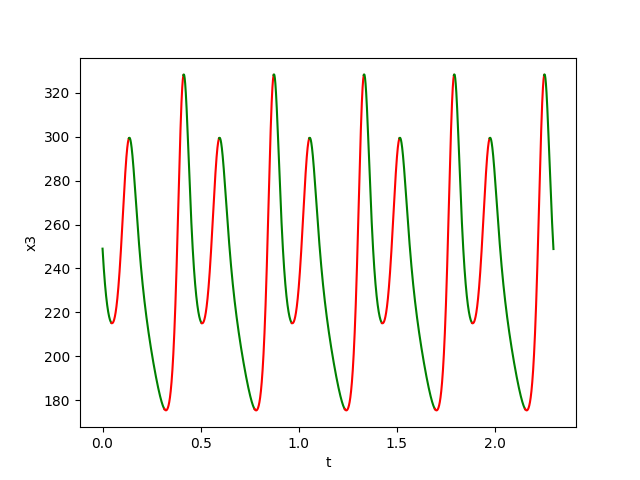
Using the figures shown below, we check that:
- \(B((i_0+1)T)\subset B(i_0T)\) for \(i_0=2\)
- and \(\Sigma_{i=1}^k\lambda_i\approx\) \(-6.304 < 0\).
Then, we can conclude that the system
converges towards an attractive LC
contained in
\([B(2T),B(3T)]\).
The figures below show respectively the simulation of \(x_1(t), x_2(t), x_3(t)\) and \(\delta_{{\cal W}}(t)\) without perturbation (w=0) over 5 periods (5T=2.3) for dt=0.00001.
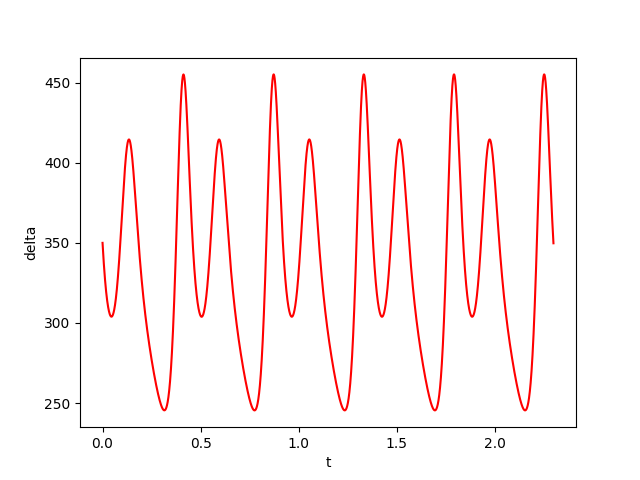
References:
[1] LORENZ, Edward N. Deterministic nonperiodic flow. Journal of atmospheric sciences, 1963, vol. 20, no 2, p. 130-141.
[2] TUCKER, Warwick. Computing accurate Poincaré maps. Physica D: Nonlinear Phenomena, 2002, vol. 171, no 3, p. 127-137.




