Filtered Quadrics for High-Speed Geometry Smoothing and Clustering

Hélène Legrand, Jean-Marc Thiery and Tamy Boubekeur
COMPUTER GRAPHICS Forum, 2019


Filtered Quadrics for High-Speed Geometry Smoothing and Clustering

Abstract

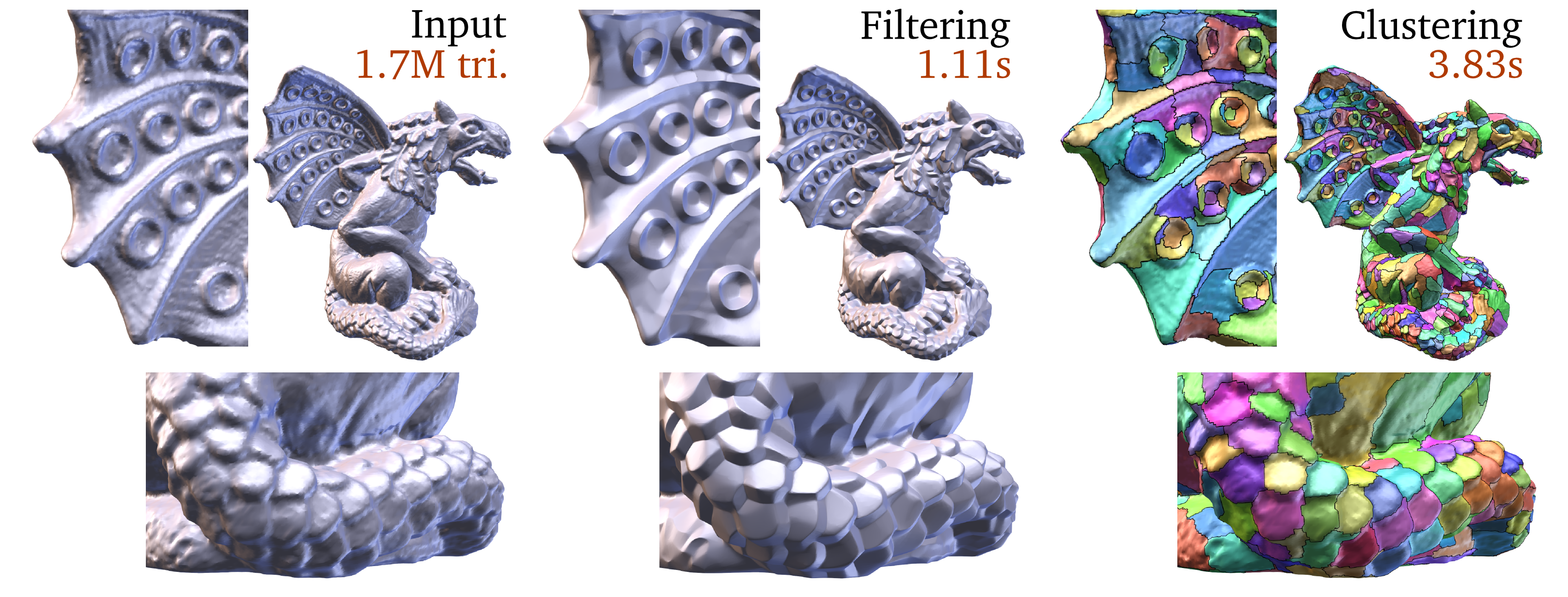
Modern 3D capture pipelines produce dense surface meshes at high speed, which challenge geometric operators to process such massive data on-the-fly. In particular, aiming at instantaneous feature-preserving smoothing and clustering disqualifies global variational optimizers and one usually relies on high-performance parallel kernels based on simple measures performed on the positions and normal vectors associated with the surface vertices. Although these operators are effective on small supports, they fail at properly capturing larger scale surface structures. To cope with this problem, we propose to enrich the surface representation with filtered quadrics, a compact and discriminating range space to guide processing. Compared to normal-based approaches, this additional vertex attribute significantly improves feature preservation for fast bilateral filtering and mode-seeking clustering, while exhibiting a linear memory cost in the number of vertices and retaining the simplicity of convolutional filters. In particular, the overall performance of our approach stems from its natural compatibility with modern fine-grained parallel computing architectures such as graphics processor units (GPU). As a result, filtered quadrics offer a superior ability to handle a broad spectrum of frequencies and preserve large salient structures, delivering meshes on-the-fly for interactive and streaming applications, as well as quickly processing large data collections, instrumental in learning-based geometry analysis.

Downloads

Bibtex

@article{LTB:2019:QGF,
	author = {Hélène Legrand and Jean-Marc Thiery and Tamy Boubekeur},
	title = {Filtered Quadrics for High-Speed Geometry Smoothing and Clustering},
	journal = {Computer Graphics Forum},
	year = {2019},
	volume = {38},
	number = {1},
	pages = {663-677},
	doi = {10.1111/cgf.13597}
}

Related projects