Un arbre couvrant de poids minimum

On considère un ensemble de points dans un plan à coordonnés entières.Ces points sont considérés comme étant les sommets d'un graphe complet valué, le poids d'une arête étant la distance euclidienne entre ses extrémités. Il s'agit de déterminer un arbre couvrant de poids minimum dans ce graphe, autrement dit de relier les points avec des segments de droite de façon à avoir un graphe connexe, en faisant en sorte que la somme des longueurs des segments soit minimum.

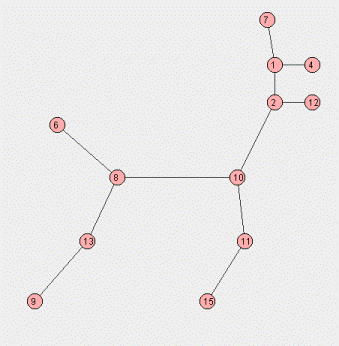
Si les points sont les points en rose ci-dessous, le résultat est celui représenté par la figure ; votre programme n'effectuera pas de représentation graphique, il suffira de faire afficher la liste des arêtes.

L'algorithme utilisé sera l'algorithme de Kruskal.

On utilisera des fichiers de données. Un tel fichier contient une ligne par sommet ; sur chaque ligne, il y a le numéro du sommet, puis son abscisse, puis son ordonnée. Les fichiers de données points1.txt et points2.txt pourront servir à l'exécution du programme. Le fichier points1.txt correspond au dessin ci-dessus. Pour le fichier points1.txt, le programme pourrait écrire sur la sortie standard :

Aretes de l'arbre couvrant de poids minimum : 
6, 7
1, 3
3, 7
5, 6
4, 7
2, 6

On définira plusieurs classes dans un paquetage nommé kruskal :

une classe Sommet modélisera un point (un sommet) ; les sommets auront des numéros entiers, pas nécessairement consécutifs ; il y aura dans la classe Sommet trois attributs privés de type int : un attribut nommé numero contiendra le numéro du sommet, deux attributs nommés abs et ord contiendront l'abscisse et l'ordonnée du sommet ; un constructeur de la classe Sommet permettra d'initialiser les attributs numero, abs et ord ;
une classe nommée Arete modélisera une Arete ; cette classe aura deux attributs privés de type Sommet nommé extr1 et extr2.
une classe nommée Kruskal qui servira à modéliser le graphe et à calculer l'arbre couvrant de poids minimum. Cette classe contiendra un attribut de type ArrayList nommé sommets qui contiendra l'ensemble des sommets du graphe et la méthode ci-dessous ;
```
public void lireFichier(String nom) throws IOException {
    File fichier = new File(nom);
    Scanner lecteur = new Scanner(fichier);
		
    while(lecteur.hasNextInt()) {
	sommets.add(new Sommet(lecteur.nextInt(), lecteur.nextInt(), lecteur.nextInt()));
    }
}
```
Toute méthode qui utilisera une méthode qui utilisera une méthode... qui utilisera la méthode lireFichier indiquera dans son en-tête throws IOException comme ci-dessus. Cela est lié au mécanisme des exceptions que vous ne verrez peut-être que plus tard.

La liste des attributs et des méthodes ci-dessus n'est pas exhaustive, vous devrez sûrement en ajouter.

L'algorithme de Kruskal nécessite de trier les arêtes du graphe par poids croissants ; il pourra être utile de faire en sorte que la classe Arete implémente l'interface java.lang.Comparable<Arete> pour utiliser une méthode statique sort de la classe java.util.Collections.

Une méthode main prendra en paramètre le nom d'un fichier de points et fera en sorte que la liste des arêtes d'un arbre couvrant de poids minimum sur ces points soit affichée à l'écran.

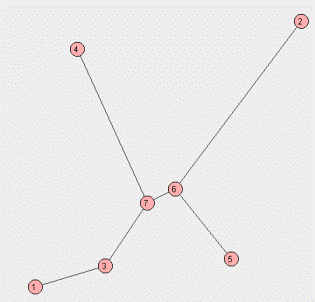
Le fichier points2.txt correspond au dessin ci-dessous.

Un arbre couvrant de poids minimum

Corrigé :