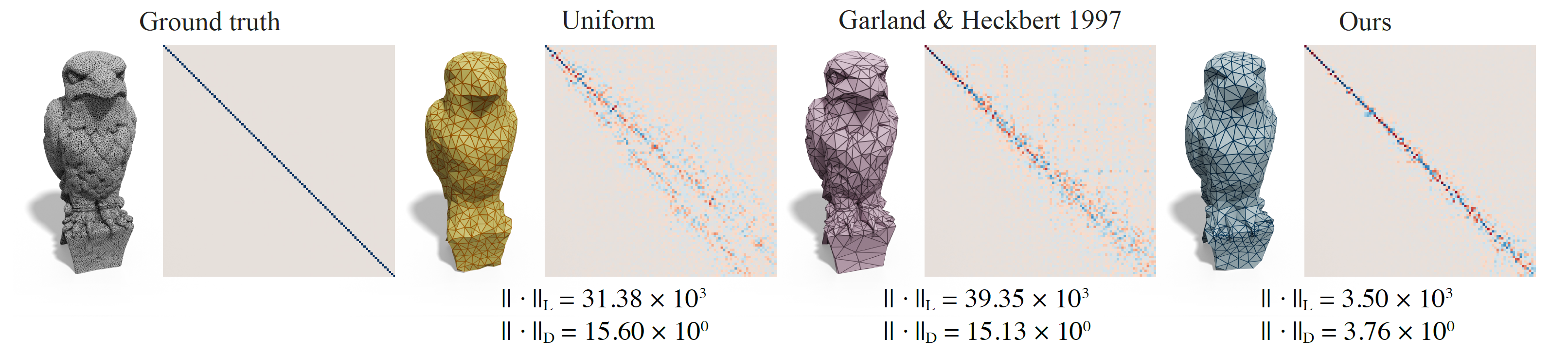
We propose to simplify a mesh using edge collapses while aiming to preserve the input eigenvectors and eigenvalues as much as possible.

Abstract

The spectrum of the Laplace-Beltrami operator is instrumental for a number of geometric modeling applications, from processing to analysis. Recently, multiple methods were developed to retrieve an approximation of a shape that preserves its eigenvectors as much as possible, but these techniques output a subset of input points with no connectivity, which limits their potential applications. Furthermore, the obtained Laplacian results from an optimization procedure, implying its storage alongside the selected points. Focusing on keeping a mesh instead of an operator would allow to retrieve the latter using the standard cotangent formulation, enabling easier processing afterwards. Instead, we propose to simplify the input mesh using a spectrum-preserving mesh decimation scheme, so that the Laplacian computed on the simplified mesh is spectrally close to the one of the input mesh. We illustrate the benefit of our approach for quickly approximating spectral distances and functional maps on low resolution proxies of potentially high resolution input meshes.

Downloads

• Manuscript: full res. (33.9MB) and low res. (8.59MB)
• Source code: git repository

Bibtex

@article{SMS:2020:LLTJBO, 
  title = "Spectral Mesh Simplification", 
  author = "Thibault Lescoat and Hsueh-Ti Derek Liu and Jean-Marc Thiery and Alec Jacobson and Tamy Boubekeur, and Maks Ovsjanikov", 
  year = "2020", 
  journal = "Computer Graphics Forum (Proc. of EUROGRAPHICS 2020)",
  number = "2",
  volume = "39",
  pages  = "315--324",
}