Abstract

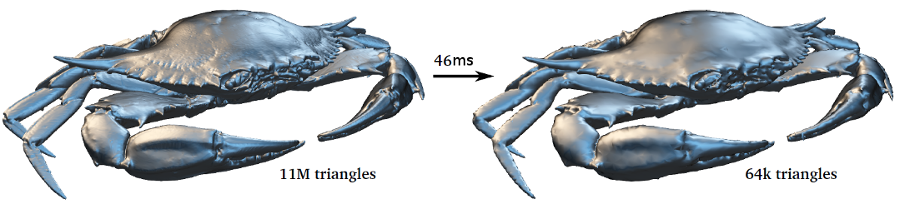
Real time geometry processing has progressively reached a performance level that makes a number of signal-inspired primitives practical for on-line applications scenarios. This often comes through the joint design of operators, data structure and even dedicated hardware. Among the major classes of geometric operators, filtering and super-sampling (via tessellation) have been successfully expressed under high-performance constraints. The subsampling operator i.e., adaptive simplification, remains however a challenging case for non-trivial input models. In this paper, we build a fast geometry simplification algorithm over a new concept: Morton Integrals. By summing up quadric error metric matrices along Morton-ordered surface samples, we can extract concurrently the nodes of an adaptive cut in the so-defined implicit hierarchy, and optimize all simplified vertices in parallel. This approach is inspired by integral images and exploits recent advances in high performance spatial hierarchy construction and traversal. As a result, our GPU implementation can downsample a mesh made of several millions of polygons at interactive rates, while providing better quality than uniform simplification and preserving important salient features. We present results for surface meshes, polygon soups and point clouds, and discuss variations of our approach to account for per-sample attributes and alternatives error metrics.

Downloads

More resources coming soon.

Bibtex

@inproceedings{LB:2015:HSGS,
  author = {Hélène Legrand and Tamy Boubekeur},
  title = {Morton Integrals for High Speed Geometry Simplification},
  booktitle ={Proceedings of the ACM SIGGRAPH/EUROGRAPHICS High Performance Graphics Conference (HPG) 2015},
  year = {2015},
  pages = {to appear}
}

Related projects

• Research on 3D Shape Approximation

Back to Tamy Boubekeur's Homepage