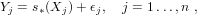
We here briefly summarized (in English) the papers which have been referenced in this synthesis.
We have considered three semi–parametric estimation problems :
In [8] the model
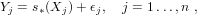
In [13] the second order properties of the discrete wavelet transform of a long memory process are studied and used to evaluate the mean square error of a wavelet log-regression estimator of the long memory parameter of a Gaussian process. A central limit theorem for this estimator is obtained in [11]. Another wavelet estimator is considered in [12], which corresponds to a Whittle contrast approach in the wavelet domain. In this paper the rate of convergence is derived for a wide class of long memory linear processes and a central limit theorem is obtained in the Gaussian case.
Finally in [6], we estimate the tail index of the durations of the pulses of a shot–noise
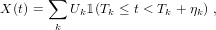
![p -α
𝔼[U01η0>t] = Lp(t) t ,](summary2x.png)
 (0,2). The estimator only depends on (possibly discretely
sampled) observations of {Xt,t = 0,…,T}. It is adapted from [12] as it relies on the long memory behavior of
this process. The consistency and the rate of covariance are investigated.
(0,2). The estimator only depends on (possibly discretely
sampled) observations of {Xt,t = 0,…,T}. It is adapted from [12] as it relies on the long memory behavior of
this process. The consistency and the rate of covariance are investigated.
We have considered three non–parametric estimation problems :
In [15, 10], we consider a shot-noise model with Poisson arrivals
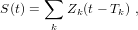
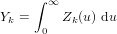
 (0,T)}. We study two estimators based on the cycles of the process S (On and Off
periods).
(0,T)}. We study two estimators based on the cycles of the process S (On and Off
periods).
In [14], we study a projection estimator of the density f of a mixing distribution with respect to a given dominating measure ν, obtained from n i.i.d. random variables X1,…,Xn having the mixture distribution
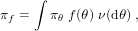
In [9], we consider a time varying auto-regressive (TVAR) model defined by
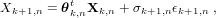 |
where
 ℕ,n ≥ 1} is a centered white noise with unit variance,
ℕ,n ≥ 1} is a centered white noise with unit variance,
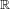 + →
+ → 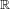 p and σk,n = σ(k∕n) with
σ :
p and σk,n = σ(k∕n) with
σ : 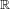 + →
+ → 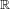 + .
+ .We give some conditions for the stability of this model as n →∞ and we study a recursive estimator from the observations Xk,n, k = 1,…,n defined by
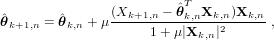 | (1) |
where μ > 0 is the step-size tuned by the user and |⋅| denotes the Euclidean norm.
In [1], we are interested in the Hausdorff dimension of the graph of a random process. A new formulation of the Frostman criterion is proposed for bounding this dimension from below. It is then shown that this formulation allows to improve some previous results obtained when the underlying process is a random wavelet series admitting some form of scaling properties at small scales.
In [3, 2], we study the modulus of continuity and the existence of the local time for linear fractional stable sheet (LFSS). The estimates on the modulus of continuity are obtained by using a random wavelet series representation of the LFSS.
In [4], we provide some new results on the dead leaves model, a model obtain by randomly superimposing random object in the space, resulting in a random tessellation. For instance we completely characterize the distribution of its boundary. In [7], these results are used to investigate some scaling dead leaves models obtained by letting converge a dead leaves model as the objects sizes distribution converges to a power law, allowing a scaling behavior in the limit, either at small scales or at large scales. We then study the regularity properties of the limit in the most interesting case, having in mind the problem of modeling natural images.
We already mentioned [13, 11, 12, 6] as they are mainly concerned with semi–parametric estimation.
In [5], we provide new sufficient conditions for the existence of some ARCH(∞) process. These
conditions include the case of the FIGARCH(0,d,0) process, d  (0,1), a process whose existence was
not rigorously proven to our knowledge. However its long range memory properties are still be
established.
(0,1), a process whose existence was
not rigorously proven to our knowledge. However its long range memory properties are still be
established.
[1] A. Ayache and F. Roueff. A Fourier formulation of the Frostman criterion for random graphs and its applications to wavelet series. Appl. Comput. Harmon. Anal., 14(1) :75–82, 2003. [pdf].
[2] A. Ayache, F. Roueff, and Xiao Y. Joint continuity of the local times of linear fractional stable sheets. C. R. Acad. Sci. Paris Sér. I Math., 2007. To appear, [pdf].
[3] A. Ayache, F. Roueff, and Xiao Y. Local and asymptotic properties of linear fractional stable sheets. C. R. Acad. Sci. Paris Sér. I Math., 2007. To appear, [pdf].
[4] C. Bordenave, Y. Gousseau, and F. Roueff. The dead leaves model : an example of a general tessellation. Advances in Applied Probability, 38(1) :31–46, mar 2006. [pdf].
[5] R. Douc, F. Roueff, and P. Soulier. On the existence of some ARCH(∞) processes. submitted, [pdf], 2006.
[6] G. Faý, F. Roueff, and P. Soulier. Estimation of the memory parameter of the infinite source Poisson process. Bernoulli, 2007. To appear, [pdf].
[7] Y. Gousseau and F. Roueff. Modeling occlusion and scaling in natural images. SIAM Multiscale Modeling and Simulation, 2007. [pdf].
[8] C. Lévy-Leduc, E. Moulines, and F. Roueff. Semiparametric frequency estimation from irregularly sampled observations. 2007. Soumis, [pdf].
[9] E. Moulines, P. Priouret, and F. Roueff. On recursive estimation for time varying autoregressive processes. Ann. Statist., 33(6) :2610–2654, 2005. [pdf].
[10] E. Moulines, F. Roueff, A. Souloumiac, and T. Trigano. Nonparametric inference of photon energy distribution from indirect measurements. Bernoulli, 2007. To appear, [pdf].
[11] E. Moulines, F. Roueff, and M.S. Taqqu. Central Limit Theorem for the log-regression wavelet estimation of the memory parameter in the Gaussian semi-parametric context. submitted, [pdf], 2006.
[12] E. Moulines, F. Roueff, and M.S. Taqqu. A wavelet Whittle estimator of the memory parameter of a non-stationary Gaussian time series. 2006. submitted, [pdf].
[13] E. Moulines, F. Roueff, and M.S. Taqqu. On the spectral density of the wavelet coefficients of long memory time series with application to the log-regression estimation of the memory parameter. J. Time Ser. Anal., 28(2), 2007. [pdf].
[14] F. Roueff and T. Rydén. Nonparametric estimation of mixing densities for discrete distributions. Ann. Statist., 33(5) :2066–2108, 2005. [pdf].
[15] T. Trigano, T. Montagu, E. Moulines, F. Roueff, and A. Souloumiac. Statistical pileup correction method for HPGe detectors. IEEE Trans. Signal Process., 2007. to appear, [pdf].