bg-body-std-rub.jpg

Webinaire Data&IA @ IMT    -     https://mintel.imt.fr/voir.php?id=5212

Vers un calcul de la pertinence

Jean-Louis Dessalles
www.dessalles.fr /slideshows

Telecom.png
Télécom Paris

Vers un calcul de la pertinence

    

  • ML:    la pertinence distingue les données du bruit
  • ML:    est pertinent ce qui est digne d’être appris/mémorisé
  • ML:    un outlier n’est pas pertinent...
  •         ... ou est très pertinent en tant qu’anomalie
 datamining_blog_tn__250_250_int.png

Vers un calcul de la pertinence

    

  • XAI: une explication est pertinente si elle peut convaincre
  • NLG: une intervention est pertinente si elle est appropriée
440px-Alan_Turing_Aged_16.jpg
  • IA:  Par définition (selon A. Turing),
    une machine intelligente
    se doit d’être pertinente.
  • → Un problème fondamental pour l’IA !
  • → Un problème fondamental en science !
  • → Le problème scientifique le plus fondamental !

Qu’y a-t-il de commun ?

    
important-stamp-imprint-exclamation-point.jpg
  • bruit
  • data utiles
  • outliers
  • anomalies
  • explication
  • intelligence

Réponse dans la Théorie algorithmique de l’information

Algorithmic Information Theory (AIT)

Intuition: Est pertinent ce qui apporte de l’information. information-1015298_1280_tr.png

    
  • L’information est ce qui reste
    quand toute redondance est éliminée
  • L’information se mesure en bits
  • L’information au sens de Shannon est une moyenne statistique sur des événements répétés.
  • Elle ne convient pas pour mesurer la pertinence

Vers un calcul de la pertinence





  • Pertinence & Machine Learning

  • Pertinence & AIQ (artificial IQ)

  • Pertinence des événements

Vers un calcul de la pertinence





  • Pertinence & Machine Learning

  • Pertinence & AIQ (artificial IQ)

  • Pertinence des événements

Algorithmic Information Theory (AIT)

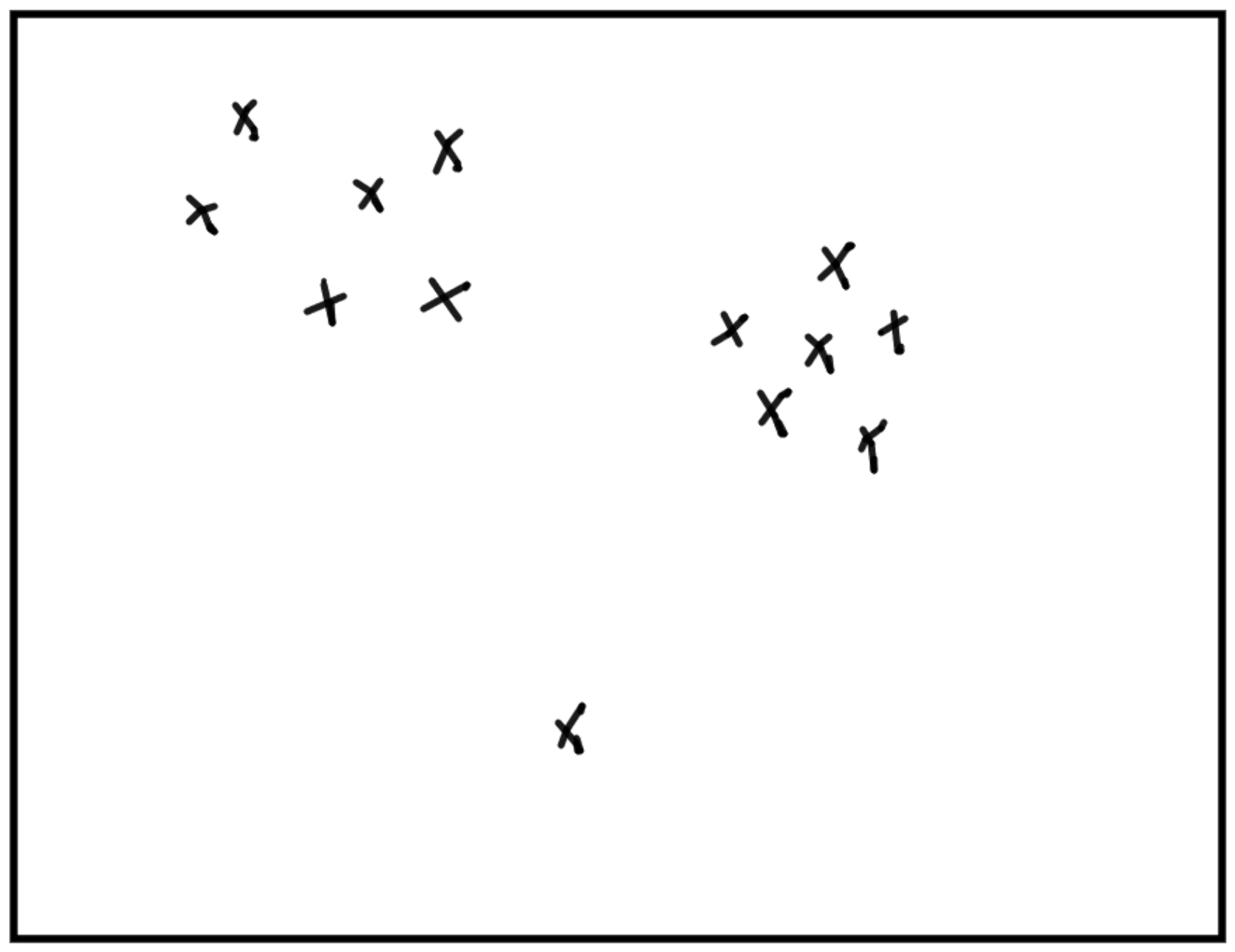Intuition: Est pertinent ce qui apporte de l’information. Dots1.png

Représenter des données de manière pertinente.

Algorithmic Information Theory (AIT)

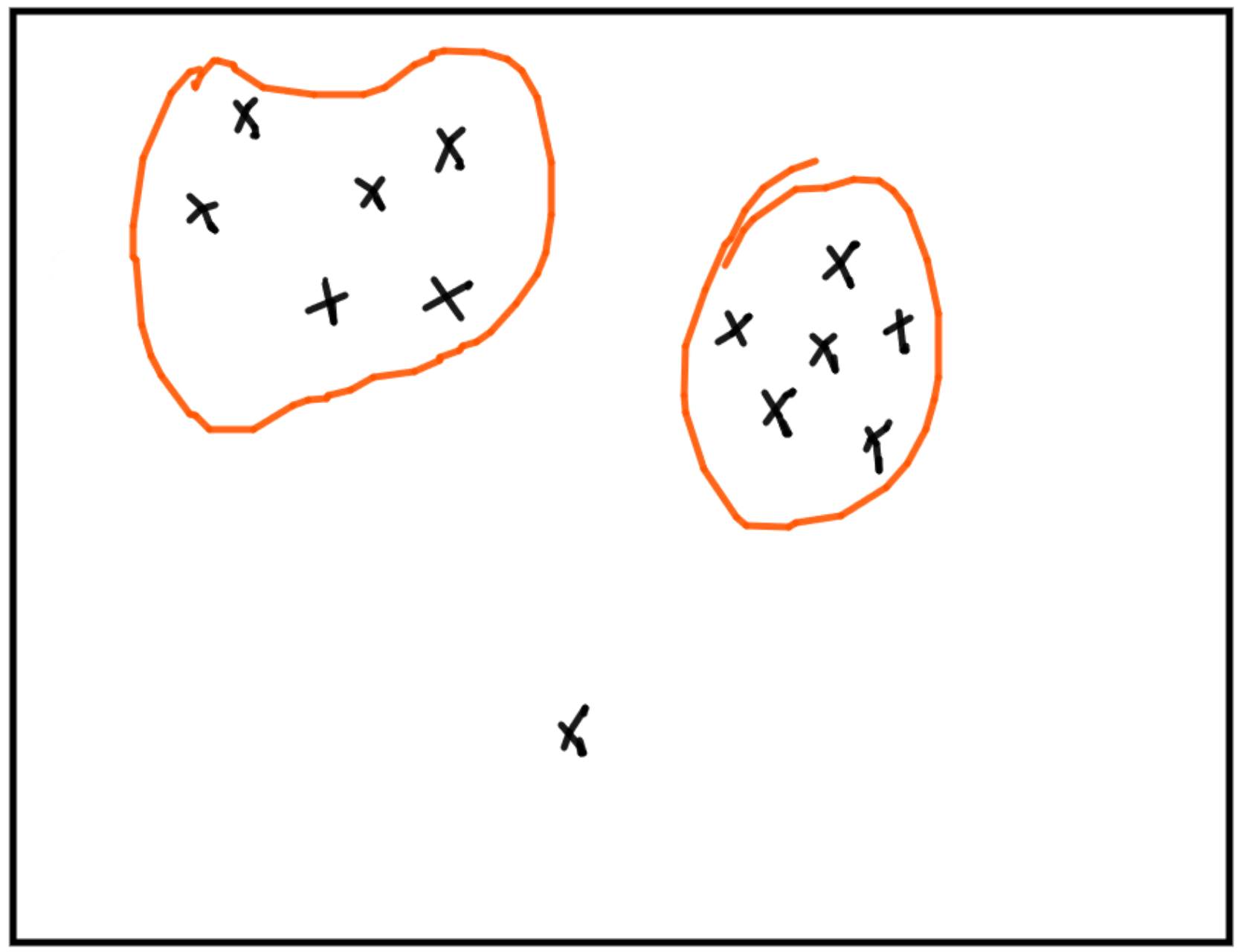Intuition: Est pertinent ce qui apporte de l’information. Dots2.png

Représenter des données de manière pertinente.

Exemple: les clusters pertinents sont ceux qui "amènent" le plus d’information.

Algorithmic Information Theory (AIT)

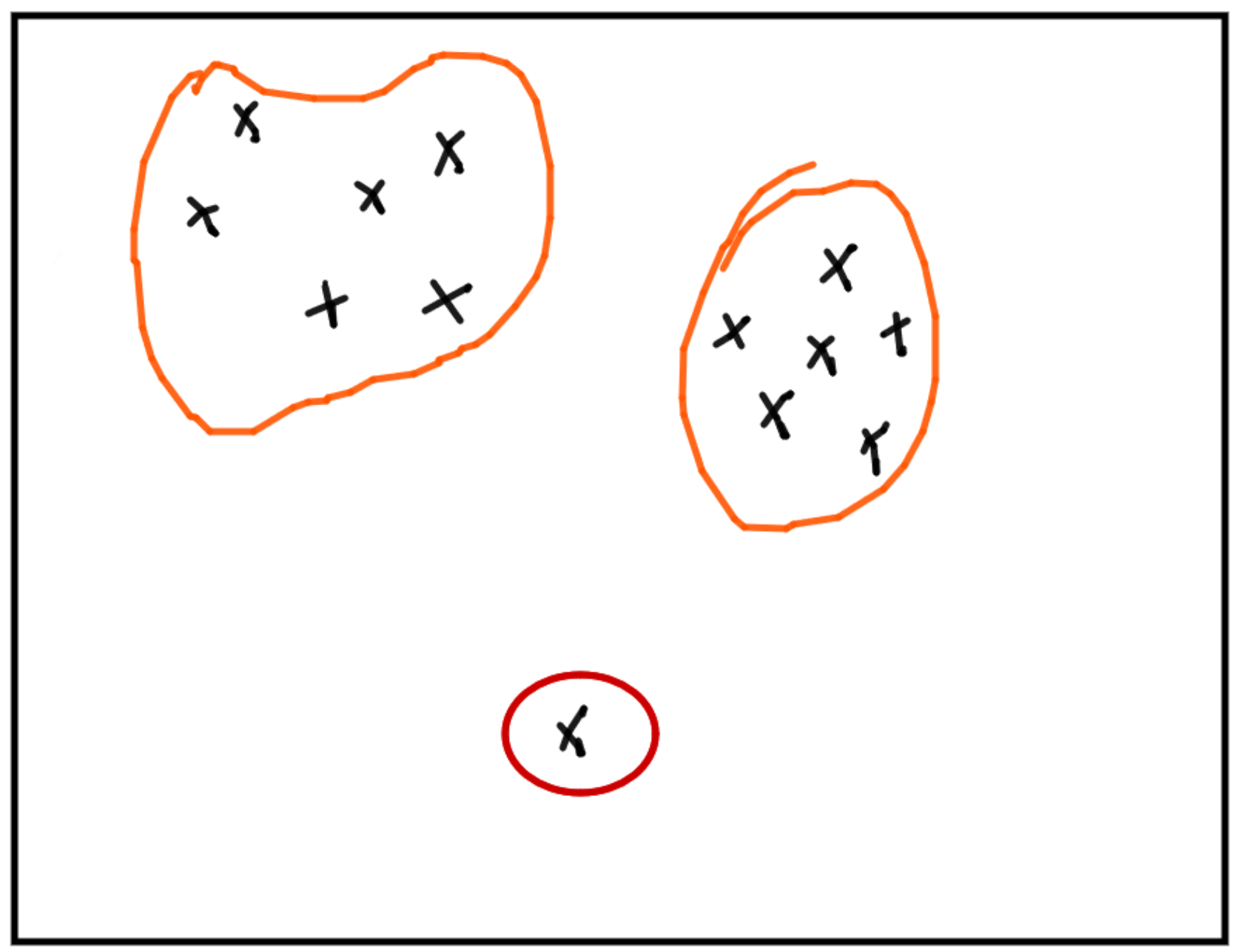Intuition: Est pertinent ce qui apporte de l’information. Dots3.png

Représenter des données de manière pertinente.

Un outlier est du bruit car il augmente artificiellement l’information
ou une anomalie car sa caractérisation demande peu d’information.

Algorithmic Information Theory (AIT)

information-1015298_1280_tr.png

    

Definition de l’information algorithmique:
Ray Solomonoff 1964, Andrei Kolmogorov 1965, Gregory Chaitin 1966

$$C(x) = min\{|p|; U(p) = x\}.$$

Taille du plus petit programme
qui engendre \(x\) sur la machine \(U\).

Thèse: La pertinence correspond à une baisse de complexité = compression



AIT & Machine learning

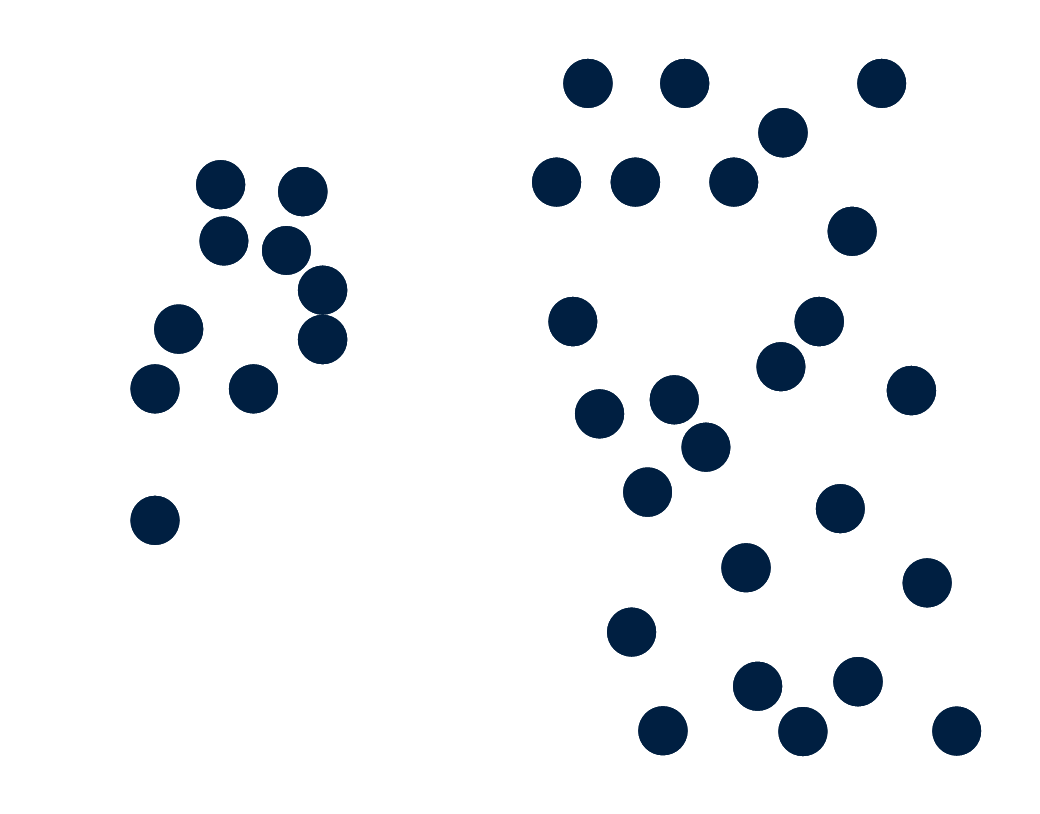Clusters8.png Prototype-based models

A prototype is a point of the input space used to provide information about the distribution of data points.

AIT & Machine learning

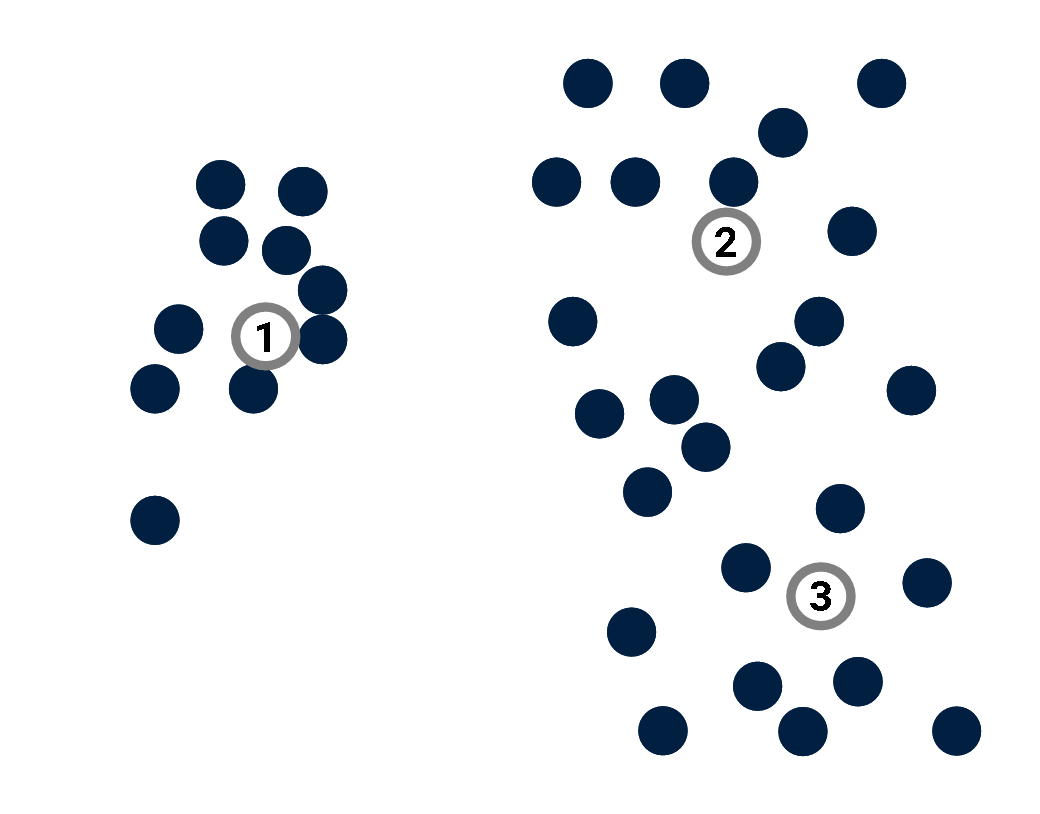Clusters9.png Prototype-based models

A prototype is a point of the input space used to provide information about the distribution of data points.

Example: K-Means algorithm.

AIT & Machine learning

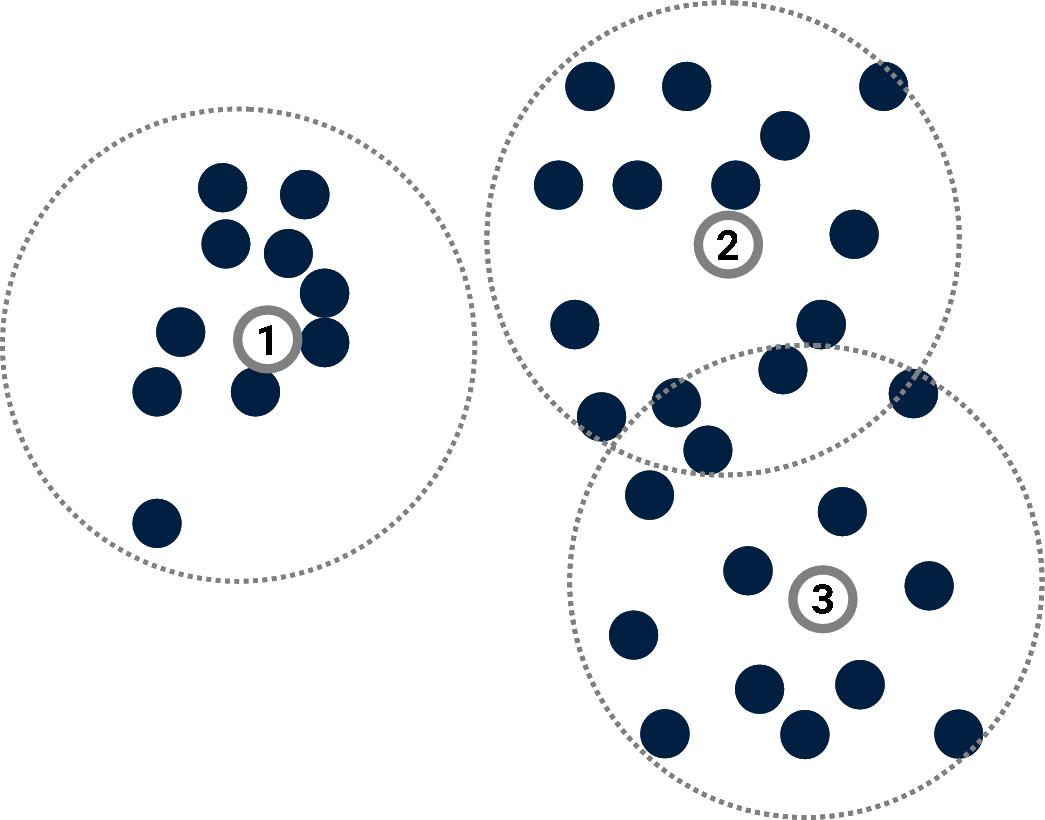Clusters10.png Prototype-based models

A prototype is a point of the input space used to provide information about the distribution of data points.

Example: K-Means algorithm.

AIT & Machine learning

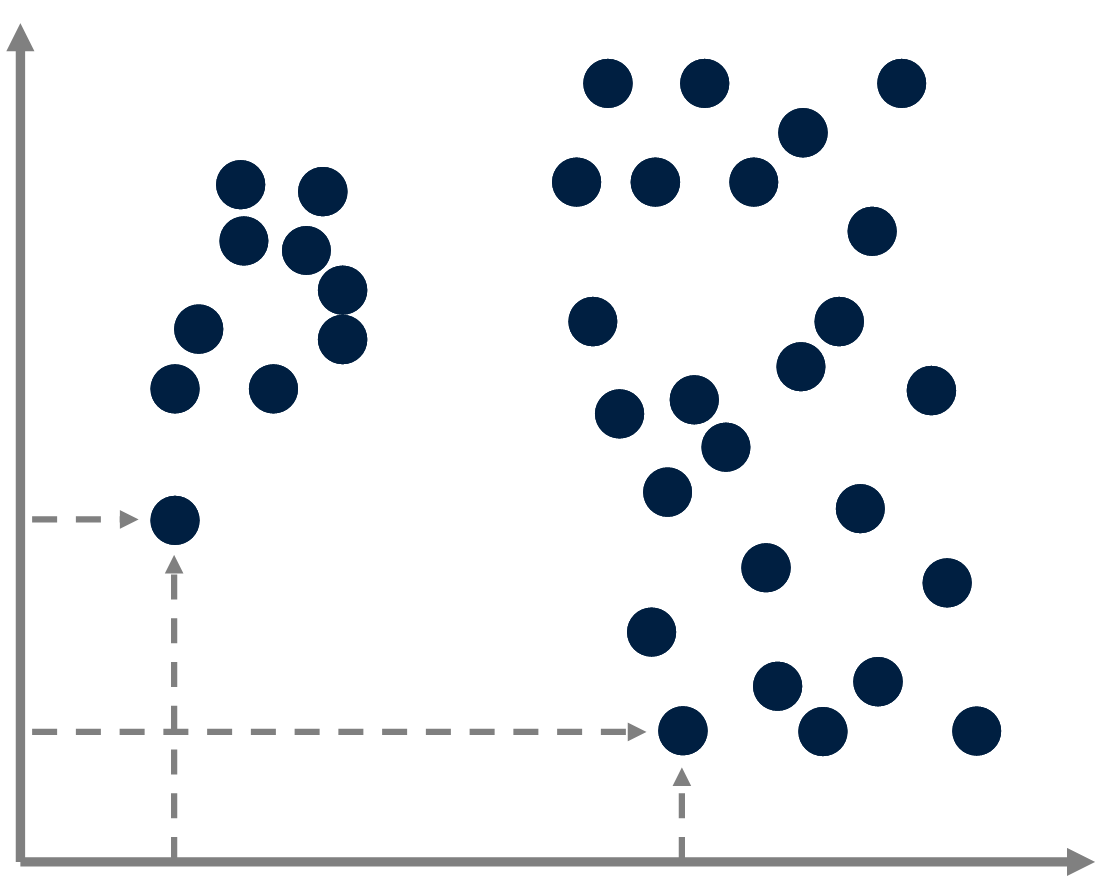Clusters11.png Compression

Prototype-based models can be seen as compression methods:

Instead of describing data points by specifying their absolute coordinates,

AIT & Machine learning

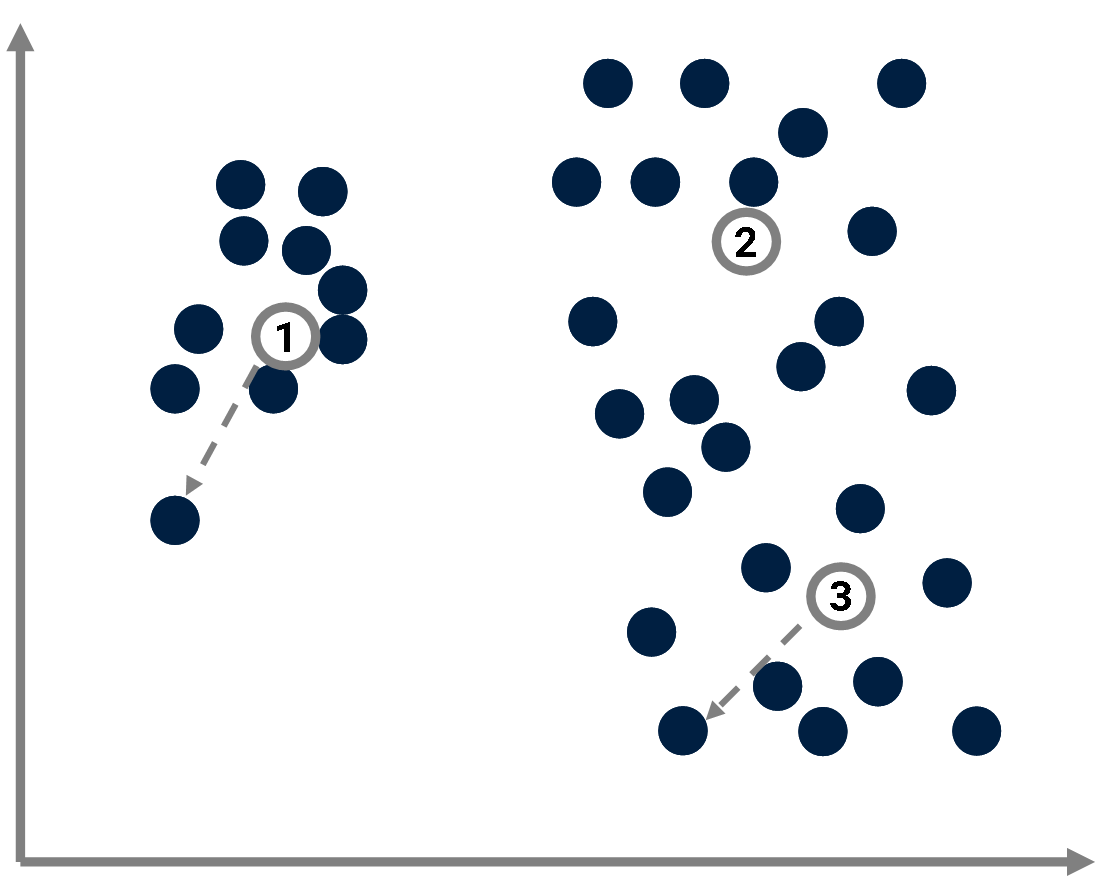Clusters12.png Compression

Prototype-based models can be seen as compression methods:

Instead of describing data points by specifying their absolute coordinates,
one considers their coordinates relative to the closest prototype.

AIT & Machine learning

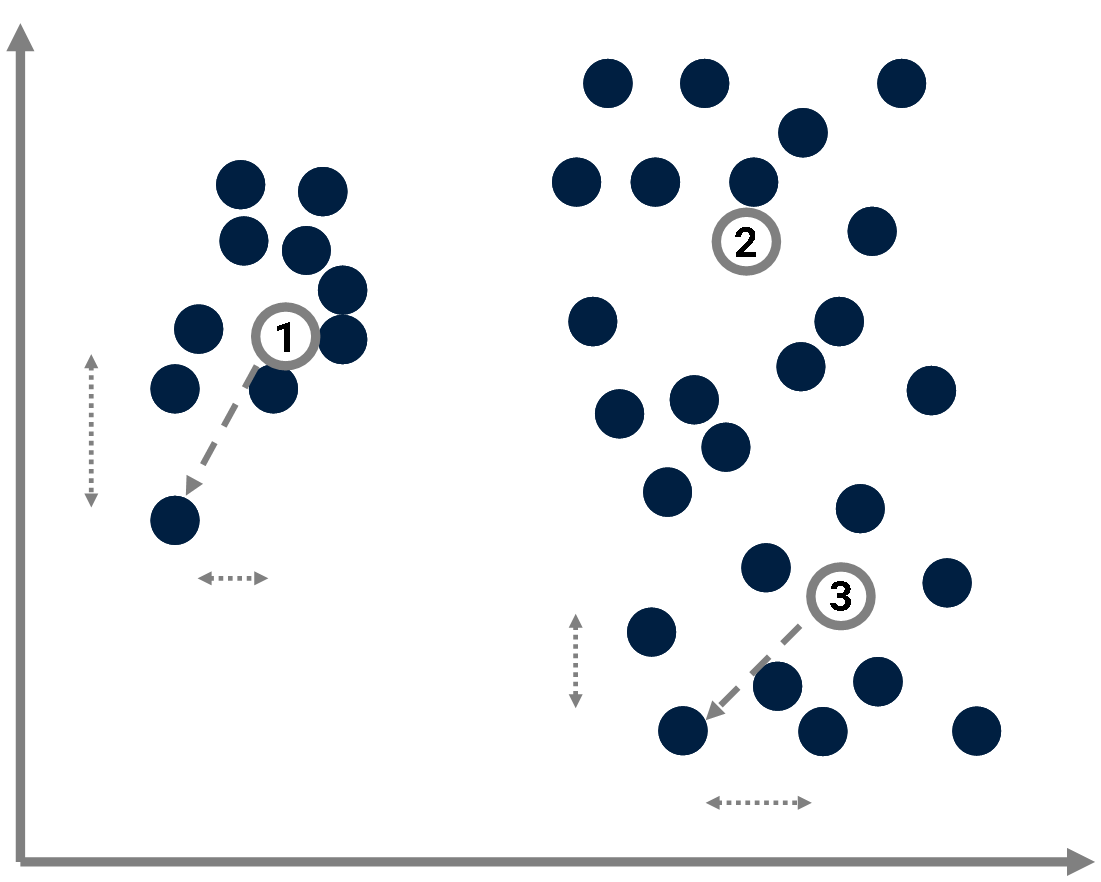Clusters13.png Compression

Prototype-based models can be seen as compression methods:

Instead of describing data points by specifying their absolute coordinates,
one considers their coordinates relative to the closest prototype.

We get smaller numbers, hence the compression.

AIT & Machine learning

Clusters11.png Compression

The complexity of a point \(x_j\) in the dataset \(X\) is bounded by the complexity of its coordinates \((x_{j_1}, \dotsc, x_{j_d})\): $$ C(x_j) \leq C(x_{j_1}) + \dotsc + C(x_{j_d}),$$ where the complexity of coordinates depends on the precision \(\delta\) used to convert them into integers.
We get a "naive" upper bound of the complexity of the whole dataset \(X\): $$C(X) \leq \sum_j C(x_j).$$

AIT & Machine learning

Clusters12.png Compression

If prototypes \(\{p_k\}\) are introduced, the complexity of \(X\) is now: $$ C(X) \leq \sum_k C(p_k) + \sum_i C(x_j|\{p_k\}),$$ where: \(C(x_j|\{p_k\}) = \min_k C(x_j-p_k).\)

If the dataset exhibits some structure, suitable prototypes can be found and this estimate of \(C(X)\) will turn out to be significantly smaller that the "naive" one (hence the compression).

Conversely, and quite remarkably, this expression can be used to find the best prototype set \(\{p_k\}\) (Cilibrasi & Vitányi, 2005).

AIT & Machine learning

Clusters12.png Compression

Prototypes \(\{p_k\}\) are relevant inasmuch as they lead to compression.

AIT & Machine learning

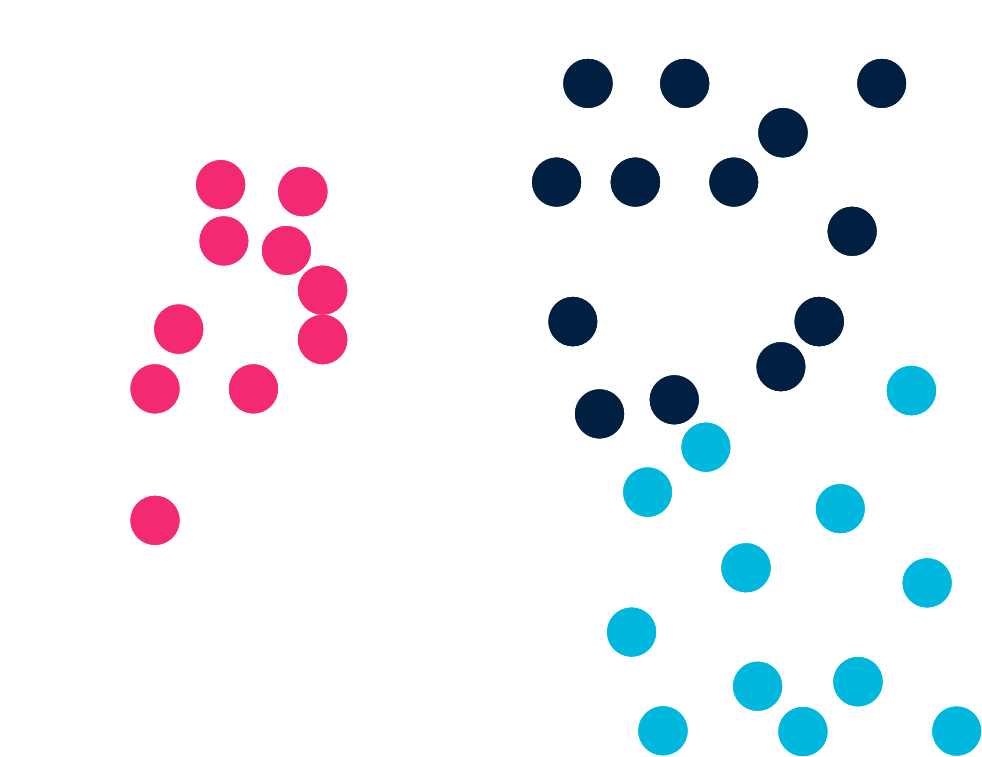Cluster1a.png Classification

Now consider a classification task as an example of supervised learning.
The problem is to associate a label (e.g. blue/red/dark) to each data point.

AIT & Machine learning

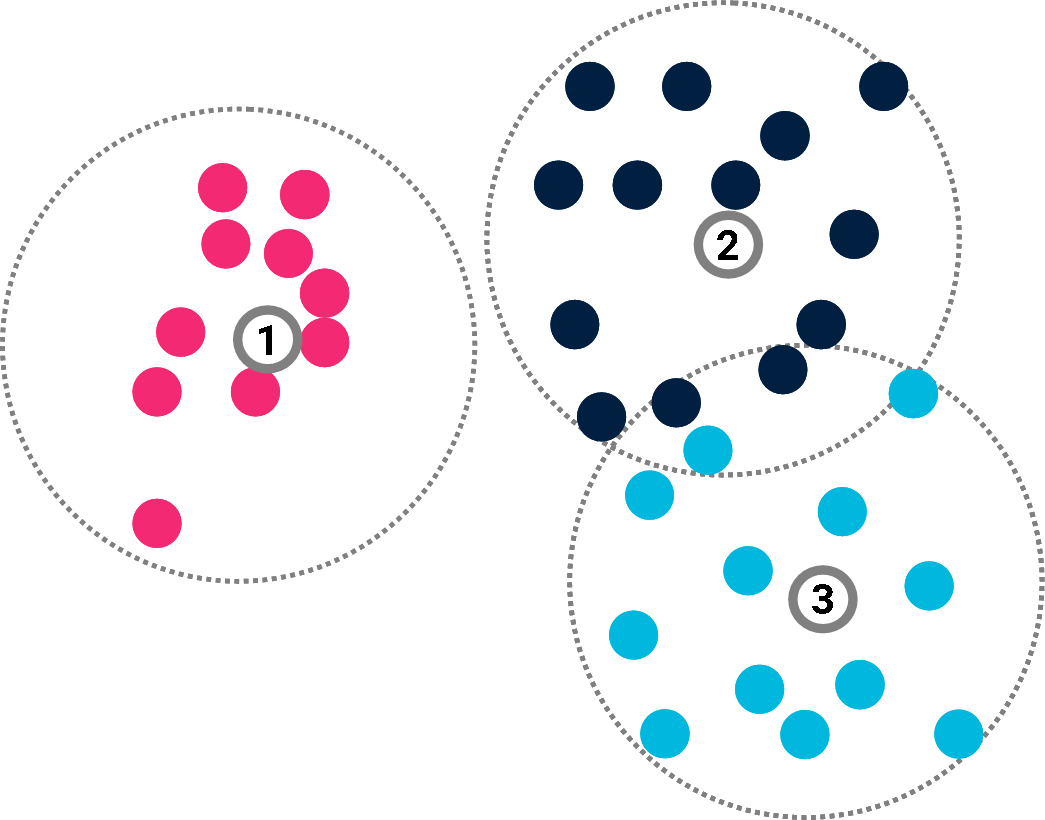Cluster3a.png Classification

Now consider a classification task as an example of supervised learning.
The problem is to associate a label (e.g. blue/red/dark) to each data point.

In doing so, they offer a compressed version of the classification.

AIT & Machine learning

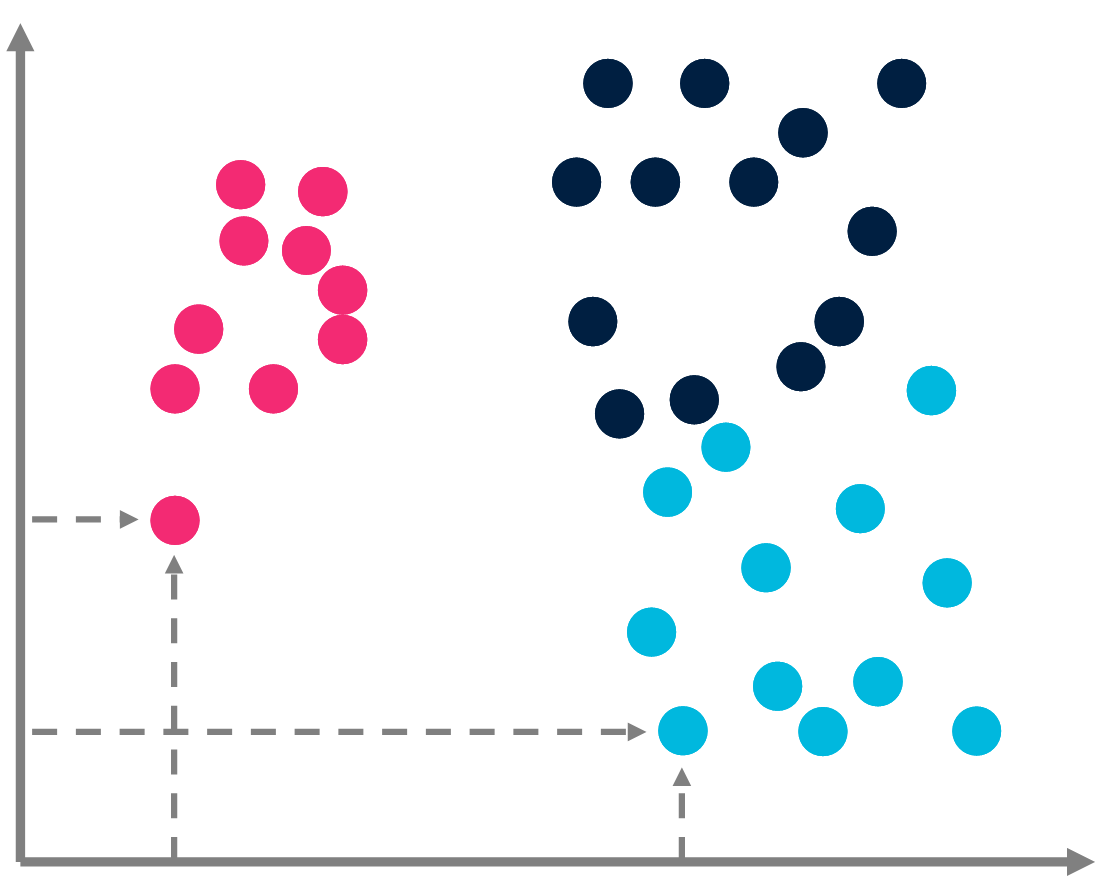Cluster4a.png Classification

In a classification task, we consider a dataset \(X\) of \(|X|\) points \(x_j\). Each \(x_j\) is supposed to belong to a class labelled as \(y_j\). The problem is to learn which label \(y_j\) taken from the set of labels \(Y\) corresponds to \(x_j\).

The complexity of the classification is bounded by the amount of information required by rote learning. $$C(\{(x_j, y_j)\} | X) \leq \sum_j C(\{y_j\}) \approx |X| \times \log(|Y|).$$

AIT & Machine learning

Cluster2a.png Classification

A prototype-based model \(\mathcal{M}\) would deduce the label of all points from those of its \(K\) prototypes \(\{p_k\}\), in the hope that: $$\beta(x_i) = y_i.$$

AIT & Machine learning

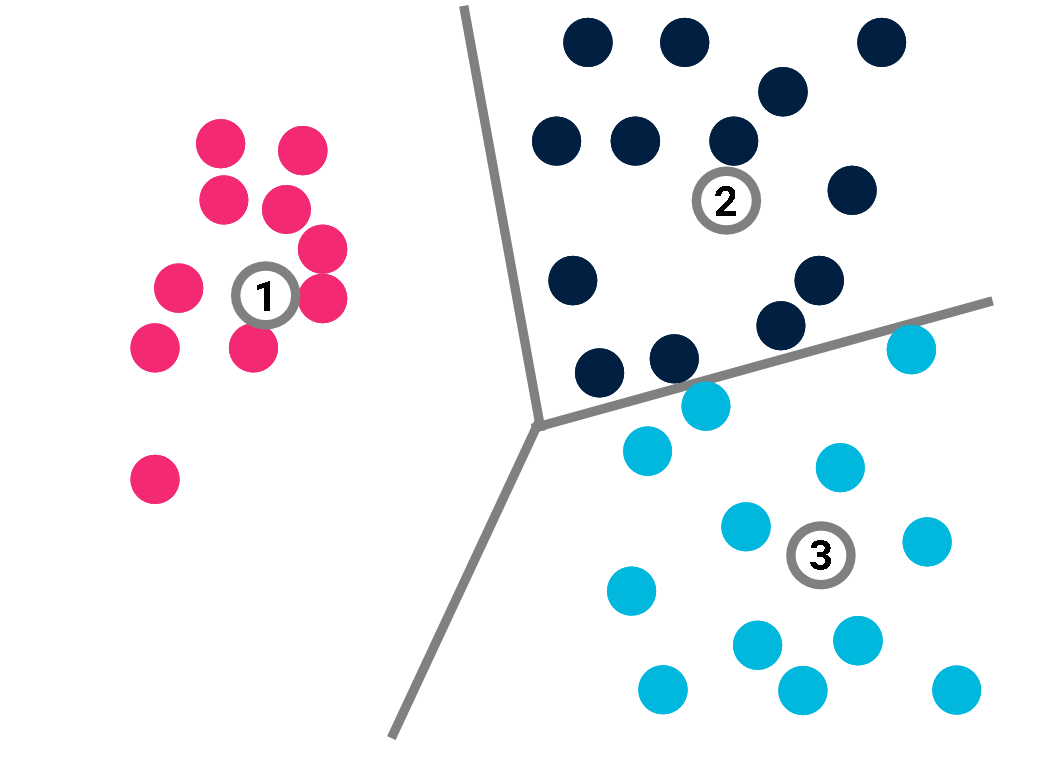Cluster7a.png Classification

A prototype-based model \(\mathcal{M}\) would deduce the label of all points from those of its \(K\) prototypes \(\{p_k\}\), in the hope that: $$\beta(x_i) = y_i.$$ The decision function \(\beta\) just returns the label of the closest prototype.

AIT & Machine learning

Cluster7a.png Classification

The complexity of the model is given by the complexity of its prototypes and their labels: $$C(\mathcal{M}) \leq \sum_k C(p_k) + K \times \log (|Y|).$$ Now: $$C(\{(x_j, y_j)\} | X) \leq C(\mathcal{M}) + \sum_{j} {C((x_j, y_j) | X, \mathcal{M})}.$$ Since the decision function \(\beta\) is just a loop over the prototypes, \(C((x_j, y_j) | X, \mathcal{M}) = 0\). So \(C(\{(x_j, y_j)\} | X)\) is found to be much smaller if \(K \ll |X|\) than if we only rely on rote learning.

AIT & Machine learning

Cluster7a.png Classification

The complexity of the model is given by the complexity of its prototypes and their labels: $$C(\mathcal{M}) \leq \sum_k C(p_k) + K \times \log (|Y|).$$ Now: $$C(\{(x_j, y_j)\} | X) \leq C(\mathcal{M}) \ll |X| \times \log(|Y|).$$ We just have to remember the prototypes and their label to retrieve all labels, hence the compression.

AIT & Machine learning

Cluster7a.png Classification

This is only true, however, if the model \(\mathcal{M}\) is perfect.

AIT & Machine learning

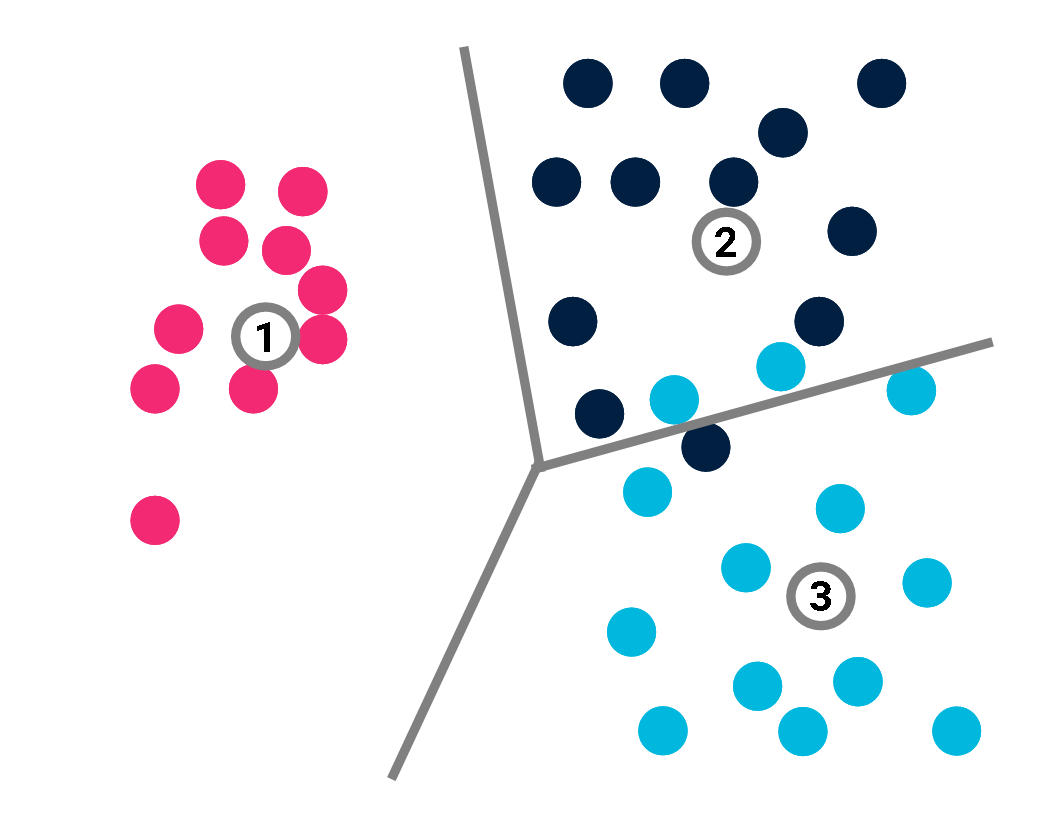Clusters7.png Classification

This is only true, however, if the model \(\mathcal{M}\) is perfect.

If not: \(C((x_j, y_j) | X, \mathcal{M}) \neq 0\).

For each misclassified point, we may just specify its index and the correct value of its label. $$\sum_{j}{C((x_j, y_j) | X, \mathcal{M})} \leq \sum_{i=1}^{|X|} (C(i) + C(y_i)) \times \mathbb{I}(y_i \neq \beta(x_i)),$$ where \(\mathbb{I}\) is a function that converts a Boolean value into 0 or 1.

AIT & Machine learning

Clusters7.png Classification

This is only true, however, if the model \(\mathcal{M}\) is perfect.

If not: \(C((x_j, y_j) | X, \mathcal{M}) \neq 0\).

More simply, if there are \(n\) misclassified points, we get: $$\sum_{j}{C(\{(x_j, y_j)\} | X, \mathcal{M})} \leq n \times (\log(|X|) +\log(|Y|)).$$

AIT & Machine learning

Clusters7.png Classification

    

To sum up: $$C(\{(x_j, y_j)\} | X) \leq \sum_k C(p_k) + K \times \log (|Y|) + n \times (\log(|X|) +\log(|Y|)).$$ If \(n\) is small, this may still represent a huge compression as compared to rote learning. The right-hand side of this inequality can be used as a loss-function to determine the best prototype-based classification.

Minimum description length (MDL)


Separate_1.png

Minimum description length (MDL)


Separate_2.png

Minimum description length (MDL)


Separate_3.png

Minimum description length (MDL)



Machine learning: find a model \(\mathcal{M}\) to compress data \(\mathcal{D} = \{d_j\}\).

$$C(\mathcal{D}) \le C(\mathcal{M}) + \sum_j{C(\mathcal{d_j} | \mathcal{M})}.$$

The most relevant model achieves the best tradeoff between its own complexity and the complexity of exceptions.

Vignette_MLCompression.png We may then keep only the model
(= lossy compression if the model isn’t perfect)
to predict future data.

Vers un calcul de la pertinence





  • Pertinence & Machine Learning

  • Pertinence & AIQ (artificial IQ)

  • Pertinence des événements

Artificial IQ

Guess what comes after:

1,2,2,3,3,3,4,4,4,4...    ?

Can you figure out a relevant answer?

Artificial IQ

Guess what comes after:

1,2,2,3,3,3,4,4,4,4,5,5,5,5,5

DL.png

1,2,2,3,3,3,4,4,4,4,4,4,3,4

Artificial IQ

Guess what comes after:

1,2,2,3,3,3,4,4,4,4,5,5,5,5,5

The most relevant answer achieves the greatest compression.

$$n^{*n}$$

\(n\) repeated \(n\) times.


The most relevant answer minimizes the overall complexity of the sequence.

Artificial IQ

Analogical equation
hofstadter_horiz.jpg

\(A\) → \(B\)

\(C\) → \(x\)

"\(A\) is to \(B\) as \(C\) is to \(x\)"

Doug Hofstadter is well-known for his original study of analogy. Let’s consider one of his favourite examples.

\(abc\) → \(abd\)
\(ppqqrr\) → \(x\)

 Have you come up with a relevant solution?

Artificial IQ

Analogical equation
hofstadter_horiz.jpg \(abc\) → \(abd\)
\(ppqqrr\) → \(x\)
Most people would instantly answer
\(ppqqrr\) → \(ppqq\)\(ss\)

Why should we consider it a more relevant solution than, say, \(ppqqrr\) → \(ppqqr\)\(d\)



Artificial IQ

Analogical equation
hofstadter_horiz.jpg \(abc\) → \(abd\)
\(ppqqrr\) → \(ppqq\)\(ss\)
\(ppqqrr\) → \(ppqqr\)\(d\)

We have to compare two rules:
  1. increment the last item
  2. replace the last letter by d

Rule 2. has two drawbacks in terms of complexity:
  1. - it introduces a constant, d.
  1. - if we do not want to lose the structure of \(ppqqrr\), the rule should read:
    "break the last item back into letters, and replace the last letter by d"

This may explain why x = ppqqss appears more relevant, and thus smarter.



Artificial IQ

Analogical equation -- Theory
hofstadter_horiz.jpg

\(A\) → \(B\)

\(C\) → \(x\)

"\(A\) is to \(B\) as \(C\) is to \(x\)"

The most relevant answer minimizes the overall complexity.

$$ x = argmin(C(A, B, C, x)).$$

Cornuéjols, A. (1996). Analogie, principe d’économie et complexité algorithmique. Actes des 11èmes Journées Françaises de l’Apprentissage. Sète, France.

Artificial IQ

Analogical equation -- Application

\(rosa\) → \(rosam\)
\(vita\) → \(x\)

Artificial IQ

Analogical equation -- Application

\(rosa\) → \(rosam\)
\(vita\) → \(vita\)\(m\)

Children learn their mother language from limited evidence. Analogy may play an important role.

A system based on the complexity principle performed better than the state of the art on lexical analogies.

Murena, P.-A., Al-Ghossein, M., Dessalles, J.-L. & Cornuéjols, A. (2020). Solving analogies on words based on minimal complexity transformation. International Joint Conference on Artificial Intelligence (IJCAI), 1848-1854.

Vers un calcul de la pertinence





  • Pertinence & Machine Learning

  • Pertinence & AIQ (artificial IQ)

  • Pertinence des événements

Relevance of events

What makes an event relevant?

Applications:
  • Personal news feed, chatbots
  • Security (e.g. nuclear plant)
  • Smart homes
  • Diagnosis
  • Abduction, CBR
  • Anomaly detection
  • Fraud detection
  • . . .

Anomaly detection

What counts as an anomaly?
Seism.png
  • outlier

Anomaly detection

What counts as an anomaly?
11_de_pique.png
  • outlier
  • impossibility

Anomaly detection

What counts as an anomaly?
illus_road_closed.png
  • outlier
  • impossibility
  • unanticipated events

Anomaly detection

What counts as an anomaly?
  • outlier
  • impossibility
  • unanticipated events
  • coincidences
mesures1.png

Anomaly detection

What counts as an anomaly?
  • outlier
  • impossibility
  • unanticipated events
  • coincidences
mesures2.png

Anomaly detection

What counts as an anomaly?
  • outlier
  • impossibility
  • unanticipated events
  • coincidences
mesures3.png

Anomaly detection

Seism.png 11_de_pique.png illus_road_closed.png mesures2.png




An anomaly is any event that is abnormally simple

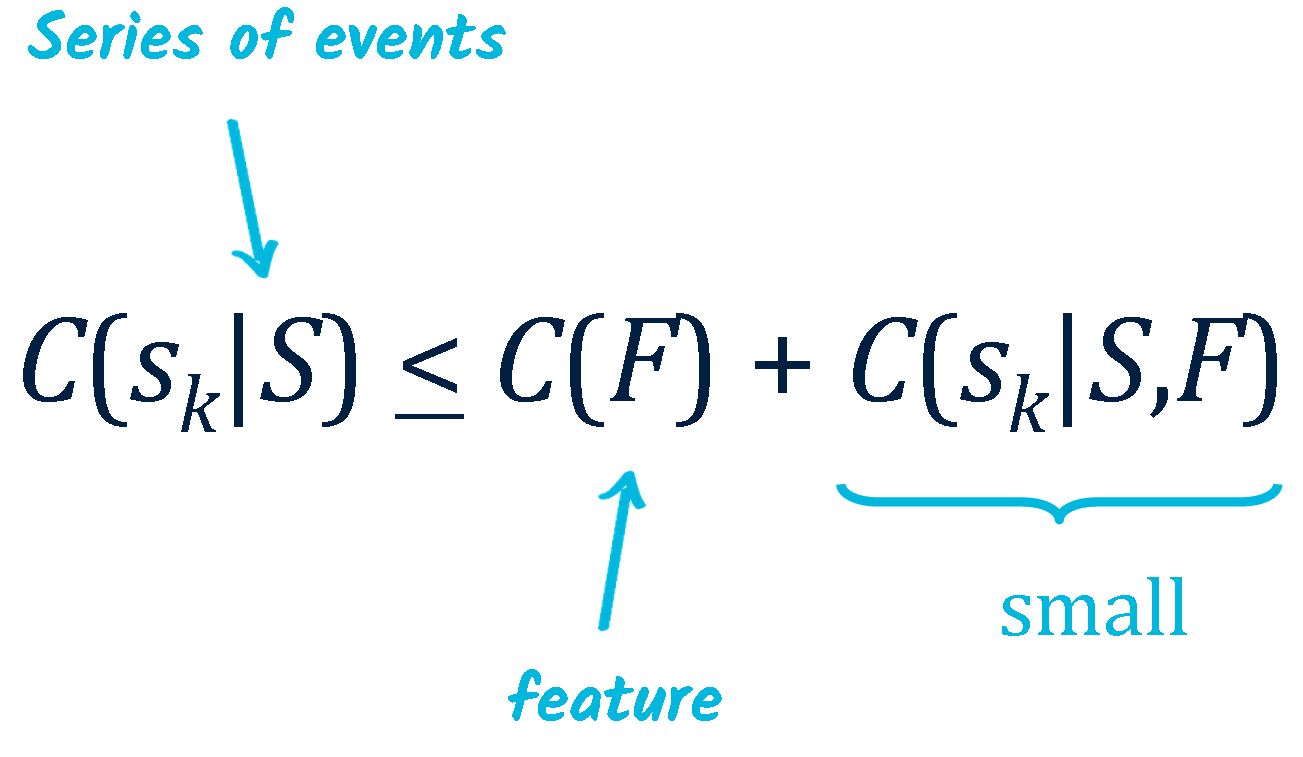
Anomaly_Simplicity.png


Anomaly detection

Plagiarism1.png

A Plagiarism story

$$ U = C(N) - C(A) $$

Unexpected events

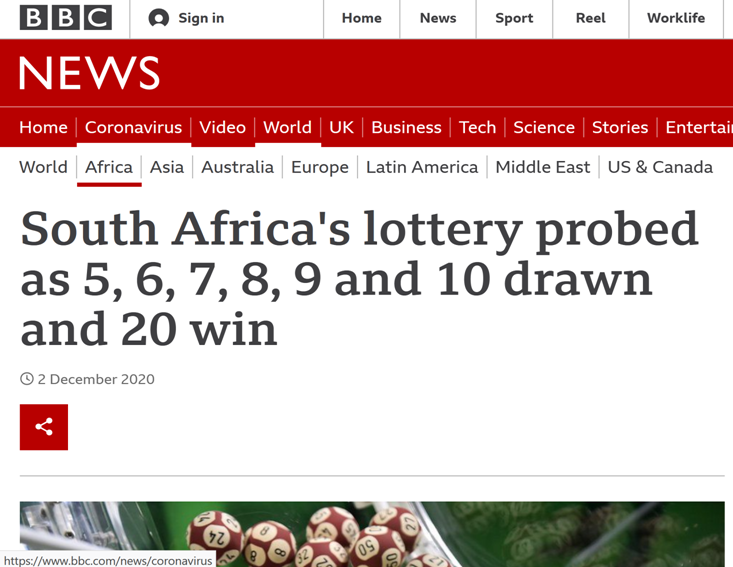
SouthAfricaLottery.png SouthAfricaLottery2.png


Simple events seem unexpected, and thus relevant.
This effect can be quantified.

Dessalles, J.-L. (2006). A structural model of intuitive probability.
ICCM-2006, 86-91. Trieste, IT: Edizioni Goliardiche.




Unexpected events

Encounter.png


Fortuitous encounter $$ U(s) = C(L) - C(p).$$


Subjective (im)probability

ordi_p_2_moins_U.png

relevance = complexity drop

$$ p = 2^{-U} $$

$$ U(s) = C_w(s) - C(s) $$

Vers un calcul de la pertinence





  • Pertinence & Machine Learning

  • Pertinence & AIQ (artificial IQ)

  • Pertinence des événements

  • Pertinence des actions

Vers un calcul de la pertinence

ordi_p_2_moins_U.png Conclusion
La pertinence
  • dans le cadre du machine learning
  • dans le cadre d’une inducion (tests QI)
  • pour les événements (anomalies, inattendu, ...)
  • (et pour les actions)

se caractérise par une baisse de complexité
(au sens de Kolmogorov).

relevance = complexity drop

Ce constat ouvre la voie à un calcul de la pertinence.


Vers un calcul de la pertinence

Pour en savoir plus... POC.png DITA_CouvertureOJ.jpg
Dessalles, J.-L. (2008). La pertinence et ses origines cognitives - Nouvelles théories. Paris: Hermes Science.
    
Dessalles, J.-L. (2019). Des intelligences très artificielles. Paris: Odile Jacob.
    
Dessalles, J.-L. (2013). Algorithmic simplicity and relevance. In Algorithmic probability and friends - LNAI 7070, 119-130. Springer.