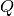Stacked A/D converter principle¶
One way to increase the dynamics of a system is to use the companding method. The companding technique compresses the signal such that signal’s maximum amplitude does not exceed system’s limitations. At the output of the system the original signal is obtained by reverse operation of expanding.
Applied to a uniform quantizer, as shown in the following figure, this leads us to the model of a floating-point quantizer.
Historically, the stacked analog-to-digital converter was introduced to increase the effective dynamic range of radar system. The following figure shows the stacked ADC principle.
This is an extension of the previously described companding principle. The compression law is piecewise linear with 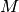 segments.
The gain increase is
segments.
The gain increase is 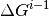 where
where 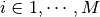 .
.
The analog to digital part of the previous scheme is split in 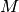 channels each performing an N-bit conversion.
channels each performing an N-bit conversion.
The expansion consists in selecting the best channel (in terms of quantification error) which is not saturated and applying the appropriate gain to this channel.
Example¶
Here is an illustrative example with: 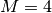 channels,
channels, 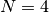 bit,
bit, 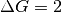
Note
The function 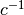 is, in this case, multivalued: the active segment (channel) give the corresponding expansion factor.
is, in this case, multivalued: the active segment (channel) give the corresponding expansion factor.
The minimum quantization error is such that:
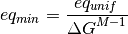
where 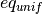 is the quantization error of the uniform quantizer
is the quantization error of the uniform quantizer