Programmer l'algorithme de Bellman

Notions utilisées

• codage d'un graphe par des listes chaînées
• l'algorithme de Bellman
• la compilation séparée

Cahier des charges

L'utilisateur dispose d'un graphe orienté d'ordre "ordre", dont les sommets sont notés 0, 1, ..., ordre - 1. Les arcs de ce graphe sont valués par des nombres entiers de signes quelconques. Le graphe est décrit dans un fichier contenant d'abord l'ordre du graphe puis la liste des arcs codés sous la forme suivante : origine extrémité longueur.
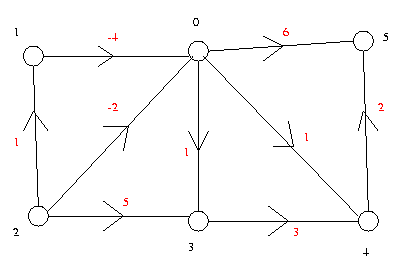
Par exemple, le graphe ci-dessous :

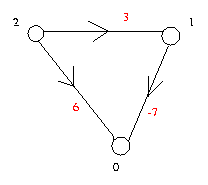
graphe1

est décrit par le fichier graphe1.don.

• Le programme demande à l'utilisateur le nom du fichier contenant le graphe.
• Si le graphe possède un circuit, le programme indique l'existence d'un circuit (sans préciser celui-ci) puis se termine.
• Si le graphe est sans circuit, le programme répète les opérations suivantes :
  • un sommet de départ est demandé, et il est indiqué de taper -1 si l'on veut terminer le programme.
  • pour chaque sommet s du graphe, si s est accessible depuis le sommet de départ indiqué, le programme indique un plus court chemin depuis le sommet de départ jusqu'à s et sa longueur; sinon le programme indique que s n'est pas accessible depuis le sommet de départ.

 bellman
Indiquez le nom du fichier décrivant le graphe
graphe1.don

Depuis quel sommet voulez-vous calculer les distances ? 
(taper -1 pour terminer) : 2

Depuis 2 :
pour atteindre 0, on peut suivre : 2 1 0    distance parcourue : -4.000000
pour atteindre 1, on peut suivre : 2 1    distance parcourue : 3.000000

Depuis quel sommet voulez-vous calculer les distances ? 
(taper -1 pour terminer) : 1

Depuis 1 :
pour atteindre 0, on peut suivre : 1 0    distance parcourue : -7.000000
le sommet 2 n'est pas accessible

Depuis quel sommet voulez-vous calculer les distances ? 
(taper -1 pour terminer) : -1

Spécifications

Numérotation topologique

Afin de savoir s'il y a un circuit et de pouvoir calculer des plus courts chemins, le programme effectuera une numérotation topologique. Nous rappelons ici une façon de calculer une numérotation topologique. On utilise une pile P, et les numéros sont calculés entre 0 et ordre - 1 et mis dans un tableau de nom num. On calcule en même temps un tableau donnant la réciproque de la numérotation topologique : si ce tableau est noté deNum, deNum[i] doit valoir x si et seulement si le numéro topologique de x vaut i.

• Initialiser avec la valeur ordre - 1 une variable entière numéro.
• Calculer les degrés extérieurs des sommets du graphe et les stocker dans un tableau.
• Empiler dans P les sommets de degré extérieur nul.
• Tant que P n'est pas vide :
  • Dépiler un sommet s de P.
  • Faire num[s]   <-   numéro
  • Faire deNum[numero]   <-   s
  • Faire numéro   <-   numéro - 1
  • Pour tout père t de s :
    • Décrémenter de 1 le degré extérieur de t .
    • Si le degré extérieur de t vaut 0, empiler t
• Si numéro vaut -1, le graphe ne contient pas de circuit et la numérotation topologique est terminée. Sinon, le graphe contient un circuit.

Algorithme de Bellman

• Initialiser la distance du sommet départ est à 0.
• Initialiser la distance des sommets différents de départ au plus grand entier possible (selon le langage utilisé), entier noté ici infini.
• Initialiser tous les antécédents à -1.
• Pour une variable entière numero qui varie de (num[départ] + 1) à (ordre - 1) :
  • noter pivot le sommet de numéro topologique numero
  • prendre le minimum de distance[x] + longueur(x, pivot) sur l'ensemble des sommets x qui sont pères de pivot et dont la distance ne vaut pas infini.
    Si l'ensemble des sommets x considérés est vide, on ne fait aucun traitement sur le sommet pivot ; sinon, on pose que l'antécédent de pivot est le sommet x qui atteint le minimum ci-dessus et que la distance de pivot est la valeur minimum trouvée.

Le travail à faire

• Pour les élèves qui travaillent sur les PC du centre de calcul de l'ENST, il faut créer un répertoire dans D:\user\usr\. Ce répertoire sera votre répertoire courant.
• Sauvegardez dans le répertoire courant tous les fichiers indiqués ci-dessous :
  • Des fichiers complets :
    • un fichier d'en-tête bellman.h.
    • un fichier pile.c qui permet d'empiler et de dépiler des entiers et de savoir aussi si la pile utilisée est vide.
    • pour ceux qui travailleraient sous Unix, un fichier contenant un Makefile .
  • Des fichiers à compléter (de manière à avoir une complexité en O(m), où m désigne le nombre d'arcs) :
    • un fichier construire.c qui doit contenir la fonction de lecture et de codage du graphe.
    • un fichier topo.c qui doit contenir ce qui est nécessaire à la numérotation topologique.
    • un fichier algoBellman.c qui doit contenir l'algorithme de Bellman proprement dit.
    • un fichier afficher.c qui doit contenir une fonction assurant l'affichage des plus courts chemins depuis un sommet donné.
    • un fichier bellman.c contenant le programme principal où seule la désallocation de la mémoire allouée dynamiquement reste à compléter.
  • Trois fichiers d'exemples :
    • graphe1.don (que vous voyez plus haut).
    • graphe2.don (que vous voyez plus bas).
    • graphe3.don (que vous voyez plus bas).
  
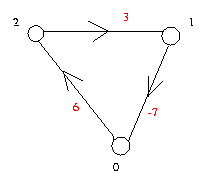
  graphe2

  
  graphe3

• Pour les élèves qui travaillent sur les PC du centre de calcul de l'ENST, après avoir activé bcw, créez un nouveau projet ; pour cela :
  • dans le menu File, choississez New puis Project
  • dans la fenêtre qui vient d'apparaître, indiquez dans "Project Path and Name" le chemin suivi du nom de votre projet (par exemple :
    D:\user\usr\anne\bellman.ide)
    et, par ailleurs, cochez console dans la case "Target Model". Faites alors OK.

    une fenêtre définissant votre projet apparaît ; il faut retirer les fichiers .cpp, .def et .rc et mettre à la place tous les fichiers .c que vous avez récupérés.

    Vous pouvez ouvrir les fichiers du projet en cliquant dessus.

   

• Pour chaque fonction à compléter :
  • complétez la fonction
  • compilez le fichier contenant la fonction (sous Unix : gcc -c fichier.c)
  • à condition d'avoir déjà complété les fonctions précédentes (par exemple, avoir déjà complété les fonctions contruire et calculDegreExt si vous travaillez actuellement sur la fonction triTopologique), testez la nouvelle fonction que vous venez de compléter :
    • Si vous êtes sous Unix, utilisez la commande make, puis, si tous se passe bien, la commande bellman.
    • Si vous êtes sur les PC du centre de calcul de l'ENST, il vous suffit d'activer run.
  • Appelez l'enseignant avant la fin de la séance pour qu'il puisse apprécier votre travail.

  Corrigé

  
  Le corrigé sera disponible après la fin du TP sous la forme des cinq fichiers suivants :
• un fichier construire.c.
• un fichier topo.c.
• un fichier algoBellman.c.
• un fichier afficher.c.
• un fichier bellman.c.