Simulation¶
Construction de variables aléatoires de loi exponentielle¶
où \(U\) est une uniforme sur \([0,1]\)
la fonction map applique la fonction \(\exp(-x)\) à tous les points de la liste /bins/, ce qui permet de tracer la densité théorique sur l’histogramme
la variable /bins/ représente le nombre d’intervalles sur lequel est construit l’histogramme
%matplotlib inline
from numpy import *
import numpy as np
import matplotlib.pyplot as plt
n=3
plt.clf()
tableau=-log(np.random.rand(10**n))
counts, bins = np.histogram(tableau,bins=30)
y=map(lambda x: exp(-x),bins+bins[1]/2)
plt.hist(bins[:-1], bins, weights=counts,density=True)
plt.plot(bins,list(y))
plt.show()
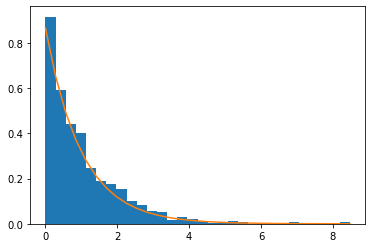
Loi de Laplace¶
Selon le texte 3 du rapport de la préparation agreg marocaine, la loi de Laplace qui a pour densité
\[\frac12 \exp(-|x|)\]
se construit comme le produit d’une variable aléatoire de Bernoulli de paramètre \(1/2\) et d’une autre variable aléatoire indépendante de loi exponentielle de paramètre \(1\).
On utilise ce schéma pour simuler de telles variables et on compare l’histogramme empirique ainsi obtenu à la densité théorique.
from numpy import *
import numpy as np
import matplotlib.pyplot as plt
n=5
plt.clf()
def bernoulli(p):
if np.random.rand()<=p:
return 1
else:
return -1
v=[bernoulli(0.5) for k in range(10**n)]
y=-log(np.random.rand(10**n))
tableau=y*v
counts, bins = np.histogram(tableau,bins=50)
y=map(lambda x: 0.5*exp(-abs(x)),bins)
plt.hist(bins[:-1], bins, weights=counts,density=True)
plt.plot(bins,list(y))
plt.show()
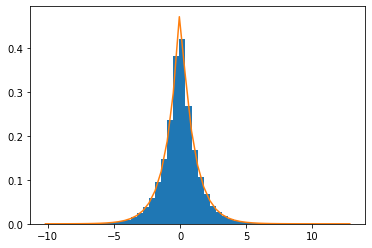
Loi gaussienne par rejet¶
On voit assez facilement que
\[\sup_{x\in\mathbf R} \frac{\exp(-x^2/2)/\sqrt{2\pi}}{\exp(-|x|)/2}=\sqrt{e}\]ce qui revient à dire que
\[\frac{1}{\sqrt{2\pi}}\exp(-\frac{x^2}{2})\le \sqrt{e}\ \frac{1}{2}\exp(-|x|)\]donc on peut appliquer la méthode du rejet pour simuler une gaussienne à partir de la simulation d’une loi de Laplace.
Comme \(\sqrt{e}\simeq 1.65\), il faudra en moyenne \(1.65\) tirages de la loi de Laplace, soit plus de 3 appels au générateur aléatoire, pour un tirage de gaussienne. C’est moins performant que la méthode de Rayleigh.
def laplace():
return -bernoulli(0.5)*log(np.random.rand())
def f(x):
return exp(-x**2/2)/sqrt(2*pi)
def g(x):
return 0.5*exp(-abs(x))
def gaussienne():
y=laplace()
u=np.random.rand()
while(f(y)<=exp(0.5)*u*g(y)):
y=laplace()
u=np.random.rand()
return y
tableau=[gaussienne() for k in range(10**5)]
counts, bins = np.histogram(tableau,bins=50)
y=map(lambda x: f(x),bins)
plt.hist(bins[:-1], bins, weights=counts,density=True)
plt.plot(bins,list(y))
plt.show()
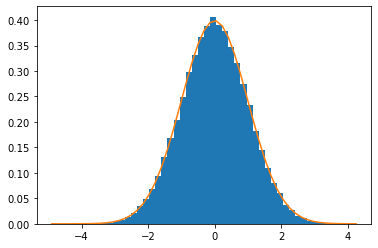
File d’attente Geo/Geo/1¶
On considère la file Geo/Geo/1 décrite dans le texte 4. Dans cette file, il y a un seul serveur et une file d’attente infinie. À chaque instant, il y a une arrivée avec probabilité \(p\) et un départ avec probabilité \(q\).
Cela signifie que le temps entre deux arrivées suit une loi géométrique de paramètre \(p\) et les temps de service une loi géométrique de paramètre \(q\).
La simulation consiste à partir d’un état \(x_0\) choisi par l’utilisateur et on utilise l’algorithme du poly.
Ici, les transitions sont simples
si \(x=0\), alors on passe à l’état \(1\) avec probabilité \(p\) et on reste en \(0\) sinon
si \(x>0\), on passe en \(x+1\) avec probabilité \(p(1-q)\), en \(x-1\) avec probabilité \(q(1-p)\), sinon on reste en \(x\).
Du point de vue de la simulation, on pose
\[r_1=p(1-q), \ r_2=r1+q(1-p)\]si le nombre aléatoire \(u\) est inférieur à \(r_1\), on augmente \(x\) de \(1\). Sinon et si \(u\) est inférieur à \(r_2\), on diminue \(x\) de \(1\). Sinon on ne fait rien.
Remarques¶
en faisant varier les valeurs relatives de \(p\) et \(q\), on constate aisément deux comportements
si \(p>q\) alors très rapidement, on quitte l’état \(0\) et la valeur du nombre de clients dans le système semble tendre vers l’infini.
si \(q<p\), on repasse très souvent par \(0\), ce qui semble dire qu’il est récurrent.
le cas limite où \(p=q\) est un peu plus compliqué à observer. On se rend compte que l’on revient à \(0\) mais que le temps entre deux passages à \(0\) est assez long. En fait, on montre que dans ce cas, la chaîne est récurrente nulle : le temps de retour à \(0\) est fini mais d’espérance infinie.
Explication¶
On peut réécrire
ce qui revient à dire que
/Le terme de service moyen est strictement inférieur au temps moyen entre deux arrivées/
Il est donc logique après un petit moment de réflexion, que le système ne sature pas. A contrario, si \(q>p\), il arrive plusieurs clients pendant la durée d’un service
from numpy import *
import numpy as np
import matplotlib.pyplot as plt
def transition(x,p,q):
if (x==0):
if (np.random.rand()<=p):
return 1
else:
return 0
else:
r1=p*(1-q)
r2=r1+q*(1-p)
u=np.random.rand()
if (u<=r1):
return x+1
else:
if (u<=r2):
return x-1
else:
return x
x=0
etats=[]
N=1000
for j in range(N):
etats+=[x]
x=transition(x,0.5,0.25)
plt.scatter(np.asarray(range(N)),np.asarray(etats),s=1)
plt.show()
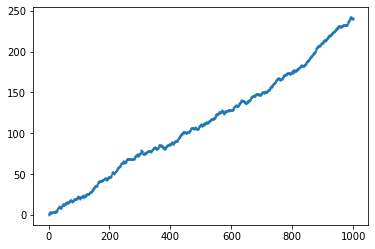
Estimation par les moyennes de Césaro¶
def transition(x,p,q):
if (x==0):
if (np.random.rand()<=p):
return 1
else:
return 0
else:
r1=p*(1-q)
r2=r1+q*(1-p)
u=np.random.rand()
if (u<=r1):
return x+1
else:
if (u<=r2):
return x-1
else:
return x
N=100000
cumul=0
x=0
for j in range(N):
x=transition(x,0.5,0.6)
if (x==2):
cumul +=1
cumul/N
0.18486
Estimation directe¶
pas ce qui était demandé
N=100000
x=0
K=1000
cumul=0
for k in range(K):
for j in range(N):
x=transition(x,0.5,0.6)
if(x==2):
cumul+=1
cumul/K
0.18
Calcul algébrique de la probabilité stationnaire¶
p=0.5
pbar=0.5
q=0.6
qbar=1-q
A=np.array([[pbar-1,q*pbar,0,0],[p,p*q+pbar*qbar-1,q*pbar,0],[0,p*qbar,p*q+pbar*qbar-1,q],[1,1,1,1]])
np.linalg.solve(A,np.array([0,0,0,1]))
array([0.24107143, 0.40178571, 0.26785714, 0.08928571])
def transition(x,p,q):
if (x==0):
if (np.random.rand()<=p):
return 1
else:
return 0
elif (x==3):
if (np.random.rand()<q):
return 2
else:
return 3
else:
r1=p*(1-q)
r2=r1+q*(1-p)
u=np.random.rand()
if (u<=r1):
return x+1
else:
if (u<=r2):
return x-1
else:
return x
N=1000000
pi_=np.zeros(4)
x=0
for j in range(N):
x=transition(x,0.5,0.6)
pi_[x]+=1
pi_/N
array([0.241419, 0.401801, 0.267611, 0.089169])
Simulation régénérative¶
où - \(N_{xy}^j\) =nb de visites à \(y\) dans la \(j\)-ième excursion - \(L^j\) = longueur de la \(j\)-ième excursion
VOir Asmussen, Applied probabilities and queues
https://nextcloud.r2.enst.fr/nextcloud/index.php/s/gYSfF4AFjYX429T
page 174
def transition(x,p,q):
if (x==0):
if (np.random.rand()<=p):
return 1
else:
return 0
elif (x==3):
if (np.random.rand()<q):
return 2
else:
return 3
else:
r1=p*(1-q)
r2=r1+q*(1-p)
u=np.random.rand()
if (u<=r1):
return x+1
else:
if (u<=r2):
return x-1
else:
return x
K=1000
visites_=np.zeros((K,4))
longueurs_=np.ones(K)
k=0
while(k<K):
x=0
y=transition(x,0.5,0.6)
while(y !=x):
visites_[k,y]+=1
longueurs_[k]+=1
y=transition(y,0.5,0.6)
k+=1
for i in range(1,4):
L=np.sum(longueurs_)
print(i,np.sum(visites_[:,i])/L)
1 0.41118944735046625
2 0.26381623834432566
3 0.09756652262906527
Estimation de pi¶
On tire des points \((U_i,V_i)\) uniformément dans le carré \([0,1]\times [0,1]\). D’après la loi forte des grands nombres
%matplotlib inline
from numpy import *
import numpy as np
import scipy
from pylab import*
import pylab as pylab
N=10**2
u=2*np.random.rand(N)-1
v=2*np.random.rand(N)-1
frequence=sum(u**2+v**2<=1)*1.0/N
variance=frequence*(1-frequence)
print "estimation de pi ", 4*frequence
print "\nintervalle de confiance à 95% ",4*(frequence-1.96*sqrt(variance)/sqrt(N)),4*(frequence+1.96*sqrt(variance)/sqrt(N))
estimation de pi 2.96
intervalle de confiance à 95% 2.6161107527124465 3.3038892472875534