Sphere-Meshes:
Shape Approximation using Spherical Quadric Error Metrics
Jean-Marc Thiery, Emilie Guy and Tamy Boubekeur
Shape Approximation using Spherical Quadric Error Metrics
ACM Transaction on Graphics (Proc. SIGGRAPH Asia 2013)
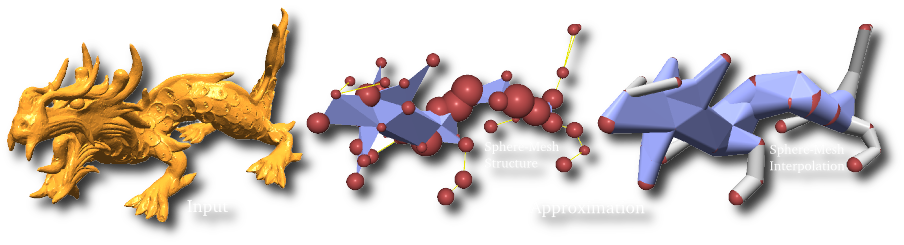
Abstract
Shape approximation algorithms aim at computing simple geometric descriptions of dense surface meshes. Many such algorithms are based on mesh decimation techniques, generating coarse triangulations while optimizing for a particular metric which models the distance to the original shape. This approximation scheme is very efficient when enough polygons are allowed for the simplified model. However, as coarser approximations are reached, the intrinsic piecewise linear point interpolation which defines the decimated geometry fails at capturing even simple structures. We claim that when reaching such extreme simplification levels, highly instrumental in shape analysis, the approximating representation should explicitly and progressively model the volumetric extent of the original shape. In this paper, we propose Sphere-Meshes, a new shape representation designed for extreme approximations and substituting a sphere interpolation for the classic point interpolation of surface meshes. From a technical point-of-view, we propose a new shape approximation algorithm, generating a sphere-mesh at a prescribed level of detail from a classical polygon mesh. We also introduce a new metric to guide this approximation, the Spherical Quadric Error Metric in R^4, whose minimizer finds the sphere that best approximates a set of tangent planes in the input and which is sensitive to surface orientation, thus distinguishing naturally between the inside and the outside of an object. We evaluate the performance of our algorithm on a collection of models covering a wide range of topological and geometric structures and compare it against alternate methods. Lastly, we propose an application to deformation control where a sphere-mesh hierarchy is used as a convenient rig for altering the input shape interactively.
Video
Downloads
Related projects
- Animated Mesh Approximation With Sphere-Meshes, Jean-Marc Thiery, Emilie Guy, Tamy Boubekeur and Elmar Eisemann, ACM Transaction on Graphics 2016
- Research projects on 3D shape approximation
Bibtex
@article{TGB:2013:SM,
author = {Jean-Marc Thiery and Emilie Guy and Tamy Boubekeur},
title = {Sphere-Meshes: Shape Approximation using Spherical Quadric Error Metrics},
journal ={ACM Transaction on Graphics (Proc. SIGGRAPH Asia 2013)},
year = {2013},
volume = {32},
number = {6},
pages = {Art. No. 178},
}


